
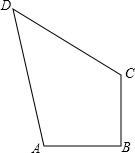
 如图,在四边形ABCD中,AB=BC=2,DC=$3\sqrt{2}$,AD=$\sqrt{26}$,∠ABC=90°,则四边形ABCD的面积是( )
如图,在四边形ABCD中,AB=BC=2,DC=$3\sqrt{2}$,AD=$\sqrt{26}$,∠ABC=90°,则四边形ABCD的面积是( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
分析 连接AC,在直角三角形ABC中得到AC的值,然后再根据:DC2+AC2=AD2,可得三角形ACD是直角三角形,最后求得三角形ACD和三角形ABC的面积和就是所求四变形的面积.
解答 解:∵连接AC,∠ABC=90°在四边形ABCD中,AB=BC=2,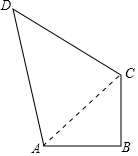
∴在直角三角形ABC中,AC2=AB2+BC2,
∴AC2=8,
又∵DC=$3\sqrt{2}$,AD=$\sqrt{26}$,
∴DC2=18,AD2=26,
∴在三角形ACD中有:DC2+AC2=18+8=26=AD2,
∴三角形ACD是直角三角形,∠DCA=90°,
∴四边形ABCD的面积=三角形DCA的面积+三角形ABC的面积=$\frac{1}{2}$DC×AC+$\frac{1}{2}$AB×BC=$\frac{1}{2}$×3$\sqrt{2}$×2$\sqrt{2}$+$\frac{1}{2}$×2×2=8,
故选:B.
点评 此题考查了勾股定理和勾股定理的逆定理,通过作辅助线可将一般的四边形转化为两个直角三角形,使面积的求解过程变得简单.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
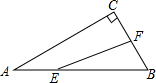 如图,在△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,F是BC的中点.若动点E以2cm/s的速度从A点出发,沿着A→B→A的方向运动,设运动时间为t(s)(0≤t≤3),连接EF,当t为1s或3s或$\frac{7}{4}$s或$\frac{9}{4}$s时,△BEF是直角三角形.
如图,在△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,F是BC的中点.若动点E以2cm/s的速度从A点出发,沿着A→B→A的方向运动,设运动时间为t(s)(0≤t≤3),连接EF,当t为1s或3s或$\frac{7}{4}$s或$\frac{9}{4}$s时,△BEF是直角三角形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1<x<7 | B. | 1<x<5 | C. | $\sqrt{7}$<x<5 | D. | 1<x<$\sqrt{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
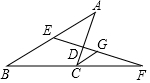 如图,在△ABC中,D是AC边上一点,且AD=2DC,E是AB边上一点,ED与BC的延长线相交于点F,且BC=CF,G是EF的中点,连接CG,若CG=2,求AB的长.
如图,在△ABC中,D是AC边上一点,且AD=2DC,E是AB边上一点,ED与BC的延长线相交于点F,且BC=CF,G是EF的中点,连接CG,若CG=2,求AB的长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
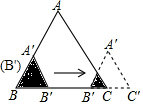 如图,边长分别为2和4的两个全等三角形,开始它们在左边重叠,大△ABC固定不动,然后把小△A′B′C′自左向右平移,直至移到点B′到C重合时停止,设小三角形移动的距离为x,两个三角形的重合部分的面积为y,则y关于x的函数图象是( )
如图,边长分别为2和4的两个全等三角形,开始它们在左边重叠,大△ABC固定不动,然后把小△A′B′C′自左向右平移,直至移到点B′到C重合时停止,设小三角形移动的距离为x,两个三角形的重合部分的面积为y,则y关于x的函数图象是( )| A. | 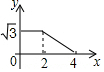 | B. | 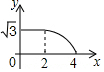 | C. | 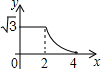 | D. | 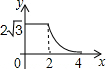 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com