

| 解:(1)△APQ∽△BCP; (2)当P为AB中点时,有AQ+BC=CQ, 证明:连接CQ,延长QP交CB的延长线于点E, 可证△APQ≌△BPE, 则AQ=BE,PQ= PE, 又因为CP⊥QE,可得CQ= CE, 所以AQ+BC=CQ; (3)当AQ=  时,有PC=3PQ, 时,有PC=3PQ,证明:在正方形ABCD中,∠A=∠B=90°,AD=BC=AB, 又因为直角三角板的顶点P在边AB上, 所以∠1+∠2=180°-∠QPC=90°, 因为Rt△CBP中,∠3+∠2=90°, 所以∠1=∠3, 所以△APQ∽△BCP, 所以  因为AQ=  , ,所以  所以AP=  ,或AP= ,或AP= (不合题意,舍去), (不合题意,舍去),所以  , ,所以PC=3PQ。 |
  |


科目:初中数学 来源: 题型:
 的另一条直角边与AD交于点Q.
的另一条直角边与AD交于点Q.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 的另一条直角边与AD交于点Q.
的另一条直角边与AD交于点Q.查看答案和解析>>
科目:初中数学 来源: 题型:
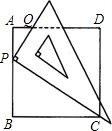
已知:如图,一块三角板的直角顶点P放在正方形ABCD的AB边上,并且使一条直角边经过点C,三角板的另一条直角边与AD交于点Q.

(1)请你写出此时图形中成立的一个结论(任选一个);
(2)当点P满足什么条件时,有AQ+BC=CQ,请证明你的结论;
(3)当点Q在AD的什么位置时,可证得PC=3PQ,并写出论证的过程.
查看答案和解析>>
科目:初中数学 来源:2008年北京市海淀区中考数学一模试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com