
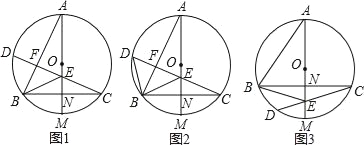
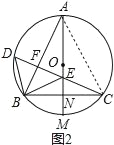
【题目】已知AM是⊙O直径,弦BC⊥AM,垂足为点N,弦CD交AM于点E,连按AB和BE.
(1)如图1,若CD⊥AB,垂足为点F,求证:∠BED=2∠BAM;
(2)如图2,在(1)的条件下,连接BD,若∠ABE=∠BDC,求证:AE=2CN;
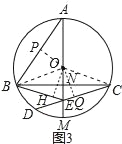
(3)如图3,AB=CD,BE:CD=4:7,AE=11,求EM的长.
【答案】(1)见解析;(2)见解析;(3)3
【解析】
(1)根据垂径定理可得BN=CN,根据垂直平分线的性质可得EB=EC,从而可得∠BED=2∠BCD,只需证明∠BAM=∠BCD即可;
(2)连接AC,如图2,易得BC=2CN,要证AE=2CN,只需证AE=BC,只需证△ABE≌△CDB,只需证BE=BD即可;
(3)过点O作OP⊥AB于P,作OH⊥BE于H,作OQ⊥CD于Q,连接OC,如图3,由AB=CD可推出OP=OQ,易证∠BEA=∠CEA,根据角平分线的性质可得OH=OQ,即可得到OP=OH,则有![]() ,从而可得
,从而可得![]() 由AE=11可求出AO、EO,就可求出AM、EM.
由AE=11可求出AO、EO,就可求出AM、EM.
解:(1)∵BC⊥AM,CD⊥AB,
∴∠ENC=∠EFA=90°.
∵∠AEF=∠CEN,
∴∠BAM=∠BCD.
∵AM是⊙O直径,弦BC⊥AM,
∴BN=CN,
∴EB=EC,
∴∠EBC=∠BCD,
∴∠BED=2∠BCD=2∠BAM;
(2)连接AC,如图2,
∵AM是⊙O直径,弦BC⊥AM,
∴![]() =
=![]()
∴∠BAM=∠CAM,
∴∠BDC=∠BAC=2∠BAM=∠BED,
∴BD=BE.
在△ABE和△CDB中,
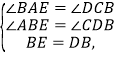
∴△ABE≌△CDB,
∴AE=CB.
∵BN=CN,
∴AE=CB=2CN;
(3)过点O作OP⊥AB于P,作OH⊥BE于H,作OQ⊥CD于Q,连接OC,如图3,
则有![]()
∵AB=CD,
∴AP=CQ,
∴![]()
∵AM垂直平分BC,
∴EB=EC,
∴∠BEA=∠CEA.
∵OH⊥BE,OQ⊥CD,
∴OH=OQ,
∴OP=OQ=OH,
∴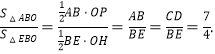
又∵![]()
∴![]()
设AO=7k,则EO=4k,
∴AE=AO+EO=11k=11,
∴k=1,
∴AO=7,EO=4,
∴AM=2AO=14,
∴EM=AM﹣AE=14﹣11=3.



科目:初中数学 来源: 题型:
【题目】某公司生产的某种产品每件成本为40元,经市场调查整理出如下信息:
①该产品90天售量(n件)与时间(第x天)满足一次函数关系,部分数据如下表:
时间(第x天) | 1 | 2 | 3 | 10 | … |
日销售量(n件) | 198 | 196 | 194 | ? | … |
②该产品90天内每天的销售价格与时间(第x天)的关系如下表:
时间(第x天) | 1≤x<50 | 50≤x≤90 |
销售价格(元/件) | x+60 | 100 |
(1)求出第10天日销售量;
(2)设销售该产品每天利润为y元,请写出y关于x的函数表达式,并求出在90天内该产品的销售利润最大?最大利润是多少?(提示:每天销售利润=日销售量×(每件销售价格-每件成本))
(3)在该产品销售的过程中,共有多少天销售利润不低于5400元,请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
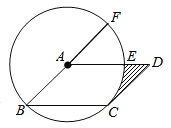
【题目】如图,在ABCD中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,交BA的延长线于点F,若弧EF的长为π,则图中阴影部分的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
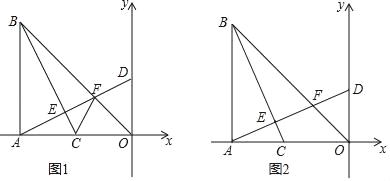
【题目】如图,在Rt△ABO中,∠BAO=90°,AO=AB,BO=8![]() ,点A的坐标(﹣8,0),点C在线段AO上以每秒2个单位长度的速度由A向O运动,运动时间为t秒,连接BC,过点A作AD⊥BC,垂足为点E,分别交BO于点F,交y轴于点 D.
,点A的坐标(﹣8,0),点C在线段AO上以每秒2个单位长度的速度由A向O运动,运动时间为t秒,连接BC,过点A作AD⊥BC,垂足为点E,分别交BO于点F,交y轴于点 D.
(1)用t表示点D的坐标 ;
(2)如图1,连接CF,当t=2时,求证:∠FCO=∠BCA;
(3)如图2,当BC平分∠ABO时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=8cm,AC=6cm,动点P从点C出发沿CB方向以3cm/s的速度向点B运动,同时动点Q从点B出发沿BA方向以2cm/s的速度向点A运动,将△APQ沿直线AB翻折得△AP′Q,若四边形APQP′为菱形,则运动时间为( )

A. 1sB. ![]()
![]() sC.
sC. ![]() sD.
sD. ![]() s
s
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在大楼AB正前方有一斜坡CD,坡角∠DCE=30°,楼高AB=60米,在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的D处测得楼顶B的仰角为45°,其中点A,C,E在同一直线上.
(1)求坡底C点到大楼距离AC的值;
(2)求斜坡CD的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
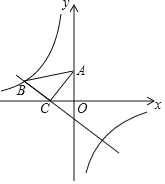
【题目】如图,在平面直角坐标系中,将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,点C坐标为(﹣1,0),点A的坐标为(0,2).一次函数y=kx+b的图象经过点B,C,反比例函数y=![]() 的图象也经过点B.
的图象也经过点B.
(1)求反比例函数的关系式;
(2)直接写出当x<0时,kx+b﹣![]() <0的解集.
<0的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
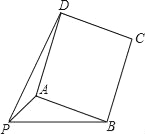
【题目】已知:PA=![]() ,PB=4,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.
,PB=4,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.
(1)如图,当∠APB=45°时,求AB及PD的长;
(2)当∠APB变化,且其它条件不变时,求PD的最大值,及相应∠APB的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在平面直角坐标系中,![]() 的斜边BC在x轴上,直角顶点A在y轴的正半轴上,
的斜边BC在x轴上,直角顶点A在y轴的正半轴上,![]() ,
,![]() .
.
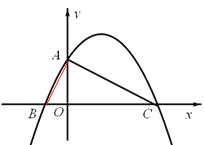
(1)求过A、B、C三点的抛物线的解析式和对称轴;
(2)设点![]() 是抛物线在第一象限部分上的点,
是抛物线在第一象限部分上的点,![]() 的面积为S,求S关于m的函数关系式,并求使S最大时点P的坐标;
的面积为S,求S关于m的函数关系式,并求使S最大时点P的坐标;
(3)在抛物线对称轴上,是否存在这样的点M,使得![]() 为等腰三角形(P为上述(2)问中使S最大时的点)?若存在,请直接写出点M的坐标;若不存在,请说明理由;
为等腰三角形(P为上述(2)问中使S最大时的点)?若存在,请直接写出点M的坐标;若不存在,请说明理由;
(4)设点M是直线AC上的动点,试问:在平面直角坐标系中,是否存在位于直线AC下方的点N,使得以点O、A、M、N为顶点的四边形是菱形?若存在,求出点N的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com