
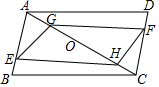
 如图,已知在平行四边形ABCD中,BE=DF,AG=CH,求证:四边形GEHF是平行四边形.
如图,已知在平行四边形ABCD中,BE=DF,AG=CH,求证:四边形GEHF是平行四边形. 分析 根据SAS可以证明△AEG≌△CFH.从而得到GE=HF,∠AGE=∠CHF.根据等角的补角相等,可以证明∠EGH=∠FHG,则GE∥HF.根据一组对边平行且相等的四边形是平行四边形即可得出结论.
解答 证明:在平行四边形ABCD中,AB∥CD,
∴∠EAG=∠FCH.AB=CD,
∵BE=DF,
∴AE=CF,
在△AEG和△CFH中,$\left\{\begin{array}{l}{AG=CH}&{\;}\\{∠EAG=∠FCH}&{\;}\\{AE=CF}&{\;}\end{array}\right.$,
∴△AEG≌△CFH(SAS).
∴GE=HF,∠AGE=∠CHF,
∴∠EGH=∠FHG,
∴GE∥HF.
∴四边形GEHF是平行四边形.
点评 此题综合运用了平行四边形的性质和判定、全等三角形的判定与性质.熟练掌握平行四边形的性质,证明三角形全等是解决问题的关键.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
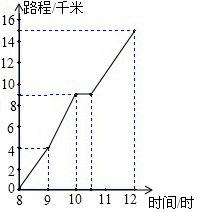 如图为一位旅行者在早晨8时从城市出发到郊外所走的路程S(单位:千米)与时间t(单位:时)的变量关系的图象.根据图象回答问题:
如图为一位旅行者在早晨8时从城市出发到郊外所走的路程S(单位:千米)与时间t(单位:时)的变量关系的图象.根据图象回答问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (5,2) | B. | (5,3) | C. | (6,2) | D. | (6,5) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
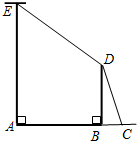 如图,AE是位于公路边的电线杆,高为10米,为了使电线CDE不影响汽车的正常行驶,电力部门在公路的另一边竖立了一根水泥撑杆BD,用于撑起电线.已知两杆之间的距离是8米,电线DE的长度为10米,求水泥撑杆BD的高度(电线杆、水泥杆的粗细忽略不计).
如图,AE是位于公路边的电线杆,高为10米,为了使电线CDE不影响汽车的正常行驶,电力部门在公路的另一边竖立了一根水泥撑杆BD,用于撑起电线.已知两杆之间的距离是8米,电线DE的长度为10米,求水泥撑杆BD的高度(电线杆、水泥杆的粗细忽略不计).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com