
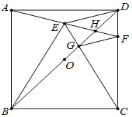
【题目】如图,正方形ABCD中,O为BD中点,以BC为边向正方形内作等边△BCE,连接AE并延长交CD于F,连接BD分别交CE、AF于G、H,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() :
:![]() ,其中正确的是__________.
,其中正确的是__________.
【答案】①③⑤
【解析】
①根据正方形的性质,等边三角形的性质以及等腰三角形的性质可先求出∠BAE=∠BEA=∠CED=∠CDE=75°,进而可得出∠DEF=30°,从而可得出∠CEH=45°;
②作BM⊥CG于M,DN⊥CG于N,由![]() ,可以得出
,可以得出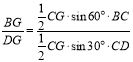 ,就有
,就有![]() 即BG=
即BG=![]() ;
;
③先利用AAS证明△DEF≌△EDG,就可以得出DF=EG,就可以得出CG=CF,得出∠CGF=75°,由∠CED=75°,就可以得出GF∥ED;
④由图可知2(OH+HD)=2OD=BD,所以2OH+DH=BD错误;
⑤由S△BEC:S△BGC=![]() ,由GE=DF=tan15°AD.设AD=CD=BC=AB=x,就有DF=EG=(2-
,由GE=DF=tan15°AD.设AD=CD=BC=AB=x,就有DF=EG=(2-![]() )x,GC=x-(2-
)x,GC=x-(2-![]() )x=(
)x=(![]() -1)x,就有
-1)x,就有![]() .综上可得出结论.
.综上可得出结论.
解:①∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠ABC=∠BCD=∠CDA=∠DAB=90°,∠ADB=∠CDB=45°.
∵△BEC是等边三角形,∴BC=BE=CE,∠EBC=∠BCE=∠BEC=60°,
∴AB=BE=CE=CD,∠ABE=∠DCE=90°-60°=30°,
∴∠BAE=∠BEA=∠CED=∠CDE=![]() ×(180°-30°)=75°,
×(180°-30°)=75°,
∴∠EAD=∠EDA=15°,
∴∠DEF=30°,
∴∠CEH=45°.
故①正确;
②作BM⊥CG于M,DN⊥CG于N,
∴∠BMC=∠DNC=90°,
∴BM=sin60°BC,DN=sin30°CD.
![]() ,
,
∴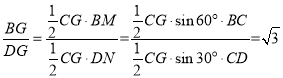 ,
,
∴BG=![]() DG.
DG.
故②错误;
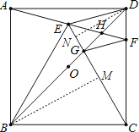
③∵∠EDC=75°,∠BDC=45°,
∴∠EDB=30°,
∴∠DEF=∠EDG=30°,
∴∠EGD=75°.
∵∠ADC=90°,∠DAF=15°,
∴∠EFD=75°,
∴∠EFD=∠EGD.
在△DEF和△EDG中,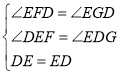 ,
,
∴△DEF≌△EDG(AAS),
∴DF=EG.
∵EC=DC,
∴EC-EG=DC-DF,
∴CG=CF,
∴∠CGF=∠CFG=75°,
∴∠CED=∠CGF,
∴GF∥ED.
故③正确;
④由图可知2(OH+HD)=2OD=BD,所以2OH+DH=BD不正确.故④错误;
⑤在Rt△ADF中,∠DAF=15°,
∴DF=tan15°AD=GE,设AD=CD=BC=AB=x,
∴CE=x,∴CG=x-GE.
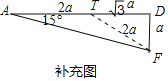
又如补充图中,在Rt△ADF中,∠A=15°,在AD上取一点T,使得AT=TF,
∴∠DTF=30°,设DF=a,则TF=TA=2a,TD=![]() a,可得tan15°=
a,可得tan15°=![]() .
.
∴GE=DF=(2-![]() )x,
)x,
∴CG=x-(2-![]() )x=(
)x=(![]() -1)x.
-1)x.
∴S△BEC:S△BGC=![]() =
=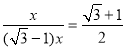 .
.
故⑤正确.
故正确的结论有:①③⑤.
故答案为:①③⑤.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
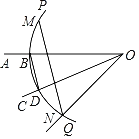
【题目】如图:已知锐角∠AOC,依次按照以下顺序操作画图:
(1)在射线OA上取一点B,以点O为圆心,OB长为半径作![]() ,交射线OC于点D,连接BD;
,交射线OC于点D,连接BD;
(2)分别以点B,D为圆心,BD长为半径作弧,交![]() 于点M,N;
于点M,N;
(3)连接ON,MN.
根据以上作图过程及所作图形可知下列结论:①OC平分∠AON;②MN∥BD;③MN=3BD;④若∠AOC=30°,则MN=![]() ON.其中正确结论的序号是_____.
ON.其中正确结论的序号是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P为△ABC边上一动点,沿着A→C→B的路径行进,点P作PD⊥AB,垂足为D,设AD=x,△APD的面积为y,图2是y关于x的函数图象,则依据图中的数量关系计算△ACB的周长为( )
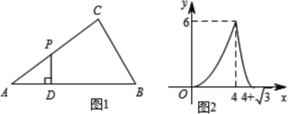

A.![]() B.15C.
B.15C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
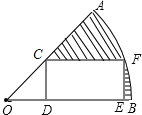
【题目】如图,在半径为![]() ,圆心角等于45°的扇形AOB内部作一个矩形CDEF,使点C在OA上,点D、E在OB上,点F在弧AB上,且DE=2CD,则:
,圆心角等于45°的扇形AOB内部作一个矩形CDEF,使点C在OA上,点D、E在OB上,点F在弧AB上,且DE=2CD,则:
(1)弧AB的长是(结果保留π)________;
(2)图中阴影部分的面积为(结果保留π)________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】襄阳市精准扶贫工作已进入攻坚阶段.贫困户张大爷在某单位的帮扶下,把一片坡地改造后种植了优质水果蓝莓,今年正式上市销售.在销售的30天中,第一天卖出20千克,为了扩大销量,采取了降价措施,以后每天比前一天多卖出4千克.第x天的售价为y元/千克,y关于x的函数解析式为![]() 且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).
且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).
(1)m= ,n= ;
(2)求销售蓝莓第几天时,当天的利润最大?最大利润是多少?
(3)在销售蓝莓的30天中,当天利润不低于870元的共有多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
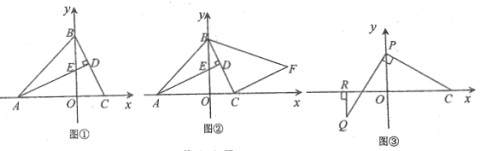
【题目】在平面直角坐标系中,![]() 的顶点
的顶点![]() ,
,![]() ,
,![]() 于
于![]() ,交
,交![]() 轴于点
轴于点![]()
(1)如图①,求点![]() 的坐标;
的坐标;
(2)如图②:将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 后得线段
后得线段![]() ,连接
,连接![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)如图③, 点![]() 为
为![]() 轴正半轴上一动点, 点
轴正半轴上一动点, 点![]() 在第二象限内,
在第二象限内,![]() 于
于![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() 垂直
垂直![]() 轴于点
轴于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“元旦大酬宾!”,某商场设计的促销活动如下:在一个不透明的箱子里放有3张相同的卡片,卡片上分别标有“10元”、“20元”和“30元”的字样,规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里摸出一张卡片,记下钱数后放回,再从中摸出一张卡片.商场根据两张卡片所标金额的和返还相等价格的购物券,购物券可以在本商场消费.某顾客刚好消费300元.
(1)该顾客最多可得到 元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于40元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com