
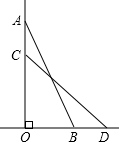
 如图,一个25m长的梯子AB,斜靠在一竖直的墙AO上,这时的AO距离为24m,如果梯子的顶端A沿墙下滑4m,那么梯子底端B向外移多少m?
如图,一个25m长的梯子AB,斜靠在一竖直的墙AO上,这时的AO距离为24m,如果梯子的顶端A沿墙下滑4m,那么梯子底端B向外移多少m? 分析 先根据勾股定理求出OB的长,再在Rt△COD中求出OD的长,进而可得出结论.
解答 解:在Rt△ABO中,
∵AB=25m,AO=24m,
∴OB=$\sqrt{A{B}^{2}-A{O}^{2}}$=$\sqrt{2{5}^{2}-2{4}^{2}}$=7m.
同理,在Rt△COD中,DO=$\sqrt{C{D}^{2}-C{O}^{2}}$=$\sqrt{2{5}^{2}-2{0}^{2}}$=15m,
∴BD=OD-OB=15-7=8(m).
答:梯子底端B向外移8m.
点评 本题考查的是勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.


 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 300(1+x)2=2000 | B. | 300+300×2x=2000 | ||
| C. | 300+300×3x=2000 | D. | 300[1+(1+x)+(1+x)2]=2000 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC交于点D、E,若四边形ODBE的面积为12,则k的值为( )
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC交于点D、E,若四边形ODBE的面积为12,则k的值为( )| A. | 6 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1题 | B. | 2题 | C. | 3题 | D. | 4题 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com