

���� ��1���Ȼ�����DEF������ֱ��������б�����ߵ���б��һ���CD=$\frac{1}{2}$AB����DE=$\frac{1}{2}$AB=BD=AD����AEB=90�㣻
��2���������ĵ㹲Բ�á�AEC=��ABC=45�㣻���������߹�������ֱ�������Σ�֤����ACH�ա�BCE����AH=BE��EC=CH�����CEH�ǵ���ֱ�������Σ��ý��ۣ�
��3����G��GH��ED����DG=x������ֱ��������30�����Ե�ֱ�DZ���б�ߵ�һ���빴�ɶ�����ʾ��AH��DH�ij�������AD=CD�ij��ý��ۣ�
���  �⣺��1����CD��AB��AC=BC��
�⣺��1����CD��AB��AC=BC��
��AD=BD��
�ߡ�ACB=90�㣬
��CD=AD=BD��
��ED=AD=BD��
���DBE=��DEB����AED=��DAE��
���AED+��DEB=��ABE+��BAE=$\frac{1}{2}$��180��=90�㣬
���AEB=90�㣻
��2����ͼ2����BEA=��BCA=90�� ��
��
��B��E��C��A�ĵ㹲Բ��
���AEC=��ABC=45�㣬
AE-$\sqrt{2}$CE=BE�������ǣ�
��C��CH��CE����AE��H�����ACH=��ECB��
�ߡ�ACH=��ECH+��AEC=90��+45��=135�㣬
��BEC=��AEB+��AEC=90��+45��=135�㣬
���ACH=��BEC��
��AC=BC��
���ACH�ա�BCE��
��AH=BE��EC=CH��
���CEH�ǵ���ֱ�������Σ�
��EH=$\sqrt{2}$EC��
��BE=AH=AE-EH=AE-$\sqrt{2}$EC��
��3����ͼ3����G��GH��ED����AD��H�����DGH=��EDC=60�㣬
���DHG=30�㣬
��DG=x����GH=AH=2x��DH=$\sqrt{3}$x��
Rt��ADC��AC=$\sqrt{2}$AD��
��2$\sqrt{2}$+$\sqrt{6}$=$\sqrt{2}$��$\sqrt{3}x+2x$����
��x=1��
��CG=2x+$\sqrt{3}x-x$=2+$\sqrt{3}$-1=1+$\sqrt{3}$��
���� �������ĵ㹲Բ�뼸�α任���ۺ��⣬�����˵���ֱ�������Ρ�ȫ�����������ĵ㹲Բ���������ж����������ĵ㹲Բ�ڼ�����Ӧ�ò��࣬Ҫ���Ⲣ���գ�����ֱ����������30���Ӧ���dz������ͣ�����ߵĹ�ϵҪ�������գ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | PA+AB | B�� | PA-AB | C�� | $\frac{AB}{PA}$ | D�� | $\frac{PA}{AB}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
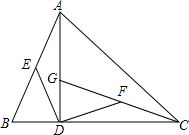 ��֪����ͼ���ڡ�ABC�У���ACB=45�㣬AD�DZ�BC�ϵĸߣ�G��AD��һ�㣬����CG����E��F�ֱ���AB��CG���е㣬��DE=DF����֤����ABD�ա�CGD��
��֪����ͼ���ڡ�ABC�У���ACB=45�㣬AD�DZ�BC�ϵĸߣ�G��AD��һ�㣬����CG����E��F�ֱ���AB��CG���е㣬��DE=DF����֤����ABD�ա�CGD���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com