
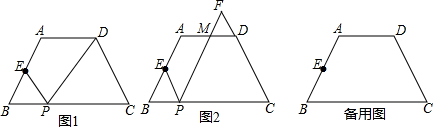
分析 (1)欲证△BEP∽△CPD,可由梯形ABCD中AB=DC,得出∠B=∠C,根据相似三角形的判断两组对应边的比相等且相应的夹角相等的两个三角形相似,证明两组对应边的比相等即可;
(2)①求y关于x的函数解析式,通过证明△BEP∽△CPF,得出比例关系即可;
②求BP的长,分为两种情况:当点F在线段CD的延长线上时,证明△BEP∽△DMF,根据S△BEP:S△DMF=4:9,得到相似比,结合y=-$\frac{1}{2}$x2+3x-4(2<x<4)求解即可,当点F在线段CD上时,同前,求得当S△DMF=$\frac{9}{4}$S△BEP时,BP的长为1.
解答 (1)证明:∵在梯形ABCD中,AD∥BC,AB=DC,
∴∠B=∠C.
BE=2,BP=2,CP=4,CD=4.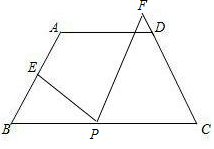
∴$\frac{EB}{CP}$=$\frac{BP}{CD}$,
∴△BEP∽△CPD.
(2)解:①∵∠B=∠C=∠EPF
∴180-∠B=180-∠EPF=∠BEP+∠BPE=∠BPE+∠CPF
∴∠BEP=∠FPC,
∴△BEP∽△CPF,
∴$\frac{EB}{CP}$=$\frac{BP}{CF}$.
∴$\frac{2}{6-x}$=$\frac{x}{y+4}$,
∴y=-$\frac{1}{2}$x2+3x-4.
②当点F在线段CD的延长线上时,
∵∠FDM=∠C=∠B,∠BEP=∠FPC=∠FMD,
∴△BEP∽△DMF,
∵S△DMF=$\frac{9}{4}$S△BEP,
∴$\frac{DF}{BP}$=$\frac{3}{2}$=$\frac{y}{x}$,
∵y=-$\frac{1}{2}$x2+3x-4,
∴x2-3x+8=0,△<0.
∴此方程无实数根.
故当点F在线段CD的延长线上时,不存在点P使S△DMF=$\frac{9}{4}$S△BEP;
当点F在线段CD上时,同理△BEP∽△DMF,
∵S△DMF=$\frac{9}{4}$S△BEP,
∴$\frac{DF}{BP}$=$\frac{3}{2}$=$\frac{y}{x}$,
∵△BEP∽△CPF,
∴$\frac{EB}{CP}$=$\frac{BP}{CF}$,
∴$\frac{2}{6-x}$=$\frac{x}{4-y}$,
∴y=$\frac{1}{2}$x2-3x+4,
∴x2-9x+8=0,解得x1=1,x2=8.
由于x2=8不合题意舍去.
∴x=1,即BP=1.
∴当S△DMF=$\frac{9}{4}$S△BEP时,BP的长为1.
点评 本题考查相似三角形综合题、等腰梯形的性质、三角形的面积、一元二次方程等知识,解题的关键是灵活运用所学知识解决问题,熟练掌握相似三角形的性质,学会构建方程解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
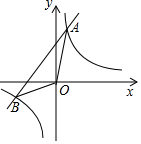 如图,点A、B是双曲线y=$\frac{k+1}{x}$(k为正整数)与直线AB的交点,且A、B两点的横坐标是关于x的方程:x2+kx-k-1=0的两根
如图,点A、B是双曲线y=$\frac{k+1}{x}$(k为正整数)与直线AB的交点,且A、B两点的横坐标是关于x的方程:x2+kx-k-1=0的两根| K | 1 | 2 | 3 | … | n(n为正整数) |
| A点的横坐标 | 1 | 1 | 1 | … | 1 |
| B点的横坐标 | -2 | -3 | -4 | … | -n-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
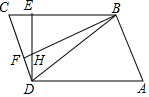 如图,在四边形ABCD中,AB=CD,AB∥CD,DE⊥BC,BF⊥CD,线段DE与BF交于点H.
如图,在四边形ABCD中,AB=CD,AB∥CD,DE⊥BC,BF⊥CD,线段DE与BF交于点H.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com