
 水果市场的甲、乙两家商店中都有批发某种水果,批发该种水果x千克时,在甲、乙两家商店所花的钱分别为y1元和y2元,已知y1、y2关于x的函数图象分别为如图所示的折线OAB和射线OC.
水果市场的甲、乙两家商店中都有批发某种水果,批发该种水果x千克时,在甲、乙两家商店所花的钱分别为y1元和y2元,已知y1、y2关于x的函数图象分别为如图所示的折线OAB和射线OC.分析 (1)利用两个函数图象的交点坐标即可解决问题.
(2)根据y2的图象在y1的下方,观察图象即可解决问题.
(3)设AB的解析式为y=kx+b,由题意OC的函数解析式为y=10x,可得方程组$\left\{\begin{array}{l}{20k+b=200}\\{300-(30k+b)=50}\end{array}\right.$,解方程组即可.
解答 解:(1)由图象可知,x=20千克时,y1=y2,
故答案为20千克.
(2)由图象可知,0<x<20时,在乙店批发比较便宜.
故答案为0<x<20.
(3)设AB的解析式为y=kx+b,由题意OC的函数解析式为y=10x,
∴$\left\{\begin{array}{l}{20k+b=200}\\{300-(30k+b)=50}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=5}\\{b=100}\end{array}\right.$,
∴射线AB的表达式y=5x+100(x≥10).
点评 本题考查一次函数的应用、二元一次方程组等知识,解题的关键是灵活运用一次函数的性质解决问题,学会利用图象解决实际问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
 如图,抛物线y=$\frac{\sqrt{3}}{3}$x2-$\frac{2\sqrt{3}}{3}$x+c与y轴交于点A(0,-$\sqrt{3}$),与x轴交于B、C两点,其对称轴与x轴交于点D,直线l∥AB且过点D.
如图,抛物线y=$\frac{\sqrt{3}}{3}$x2-$\frac{2\sqrt{3}}{3}$x+c与y轴交于点A(0,-$\sqrt{3}$),与x轴交于B、C两点,其对称轴与x轴交于点D,直线l∥AB且过点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
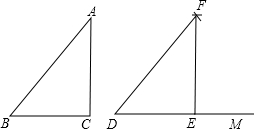 小明用如图所示的方法画出了与△ABC全等的△DEF,他的具体画法是:①画射线DM,在射线DM上截取DE=BC;②以点D为圆心,BA长为半径画弧,以点E为圆心,CA长为半径画弧,画弧相交于点F;③联结FD,FE;这样△DEF就是所要画的三角形,小明这样画图的依据是全等三角形判定方法中的( )
小明用如图所示的方法画出了与△ABC全等的△DEF,他的具体画法是:①画射线DM,在射线DM上截取DE=BC;②以点D为圆心,BA长为半径画弧,以点E为圆心,CA长为半径画弧,画弧相交于点F;③联结FD,FE;这样△DEF就是所要画的三角形,小明这样画图的依据是全等三角形判定方法中的( )| A. | 边角边 | B. | 角边角 | C. | 角角边 | D. | 边边边 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
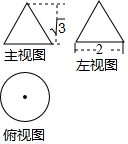 已知一个圆锥的三视图如图所示,请利用图中所给出数据,求出这个圆锥的侧面积为( )
已知一个圆锥的三视图如图所示,请利用图中所给出数据,求出这个圆锥的侧面积为( )| A. | 2π | B. | 4π | C. | $\sqrt{3}$π | D. | 2$\sqrt{3}$π |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
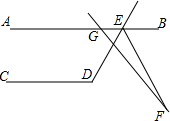 如图,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=130°,则∠F的度数是( )
如图,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=130°,则∠F的度数是( )| A. | 10.5° | B. | 9.5° | C. | 8.5° | D. | 8° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
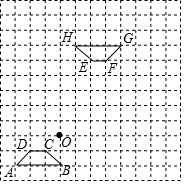 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点四边形ABCD、四边形EFGH(顶点是网格线的交点)和格点O.
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点四边形ABCD、四边形EFGH(顶点是网格线的交点)和格点O.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com