
 个单位长度的速度由点P向点O 运动,过点M作直线MN∥x轴,交PB于点N.将△PMN沿直线MN对折,得到△P1MN.在动点M的运动过程中,设△P1MN与梯形OMNB的重叠部分的面积为S,运动时间为t秒.求S关于t的函数关系式.
个单位长度的速度由点P向点O 运动,过点M作直线MN∥x轴,交PB于点N.将△PMN沿直线MN对折,得到△P1MN.在动点M的运动过程中,设△P1MN与梯形OMNB的重叠部分的面积为S,运动时间为t秒.求S关于t的函数关系式.
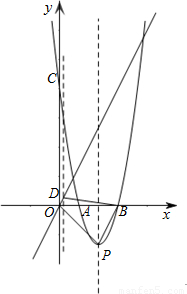 解:(1)设二次函数的解析式为y=ax2+bx+c
解:(1)设二次函数的解析式为y=ax2+bx+c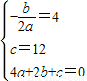 ,
, ,
,
 ,
,

 ,x2=2,(6分)
,x2=2,(6分) ,四边形OPBD为平行四边形,舍去,
,四边形OPBD为平行四边形,舍去, 时四边形OPBD为等腰梯形,(7分)
时四边形OPBD为等腰梯形,(7分) ,
, )时,四边形OPBD为等腰梯形;(8分)
)时,四边形OPBD为等腰梯形;(8分)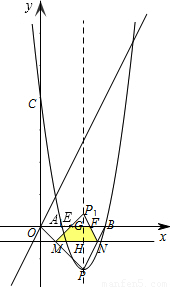 ∵运动速度为每秒
∵运动速度为每秒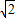 个单位长度,运动时间为t秒,则MP=
个单位长度,运动时间为t秒,则MP=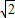 t,
t, t,
t, t,
t, t•t•
t•t• =
= t2(10分),
t2(10分),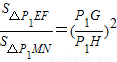 ,
,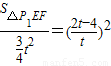 ,
, =3t2-12t+12,
=3t2-12t+12, t2-(3t2-12t+12)=-
t2-(3t2-12t+12)=- t2+12t-12,
t2+12t-12, t2,
t2, t2+12t-12.(12分)
t2+12t-12.(12分)

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2001年全国中考数学试题汇编《二次函数》(01)(解析版) 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2001年宁夏中考数学试卷(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com