
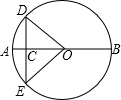
 如图,C是⊙O的直径AB上一点,过点C作弦DE,使CD=CO,若∠AOD=40°,求$\widehat{BD}$,$\widehat{AE}$的度数.
如图,C是⊙O的直径AB上一点,过点C作弦DE,使CD=CO,若∠AOD=40°,求$\widehat{BD}$,$\widehat{AE}$的度数.  金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| x | … | -3 | -2 | -1 | 1 | 2 | 3 | … |
| y | … | -2 | -3 | -6 | 6 | 3 | 2 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
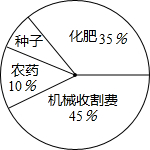 南县农民一直保持着冬种油菜的习惯,利用农闲冬种一季油菜.南县农业部门对2014年的油菜籽生产成本、市场价格、种植面积和产量等进行了调查统计,并绘制了如下统计表与统计图:
南县农民一直保持着冬种油菜的习惯,利用农闲冬种一季油菜.南县农业部门对2014年的油菜籽生产成本、市场价格、种植面积和产量等进行了调查统计,并绘制了如下统计表与统计图:| 每亩生产成本 | 每亩产量 | 油菜籽市场价格 | 种植面积 |
| 310元 | 130千克 | 5元/千克 | 500000亩 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com