
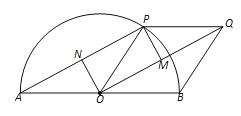
【题目】如图,已知AB为半圆O的直径,P为半圆上的一个动点(不含端点),以OP、OB为一组邻边作POBQ,连接OQ、AP,设OQ、AP的中点分别为M、N,连接PM、ON.
(1)试判断四边形OMPN的形状,并说明理由.
(2)若点P从点B出发,以每秒15°的速度,绕点O在半圆上逆时针方向运动,设运动时间为ts.
①试求:当t为何值时,四边形OMPN的面积取得最大值?并判断此时直线PQ与半圆O的位置关系(需说明理由);
②是否存在这样的t,使得点Q落在半圆O内?若存在,请直接写出t的取值范围;若不存在,请说明理由.
【答案】(1)四边形OMPN为矩形,理由见解析;(2)①当t=6秒时,四边形OMPN面积最大,此时,PQ与半圆O相切.理由见解析;②当8<t<12时,点Q在半圆O内.
【解析】
(1)先证四边形PQOA为平行四边形,再证四边形OMPN为平行四边形,根据等腰三角形三线合一,得ON⊥AP,进而即可得到结论;
(2)①由题意得S矩形OMPN=S△AOP,从而得△AOP的AO边上的高取得最大值,此时△AOP的面积取得最大值,进而即可得到t的值,根据切线的判定定理,即可得到结论;②考虑两个特殊情况:当点Q在半圆O上时,当点P与点A重合时,分别求出t的值,进而即可得到答案.
(1)四边形OMPN为矩形,理由如下:
∵四边形POBQ为平行四边形,
∴PQ∥OB,PQ=OB.
又∵OB=OA,
∴PQ=AO.
又∵PQ∥OA,
∴四边形PQOA为平行四边形,
∴PA∥QO,PA=QO.
又∵M、N分别为OQ、AP的中点,
∴OM=![]() OQ,PN=
OQ,PN=![]() AP,
AP,
∴OM=PN,
∴四边形OMPN为平行四边形.
∵OP=OA,N是AP的中点,
∴ON⊥AP,即∠ONP=90°,
∴四边形OMPN为矩形;
(2)①∵四边形OMPN为矩形,
∴S矩形OMPN=ON·NP=ON·![]() AP,即S矩形OMPN=S△AOP.
AP,即S矩形OMPN=S△AOP.
∵△AOP的底AO为定值,
∴当P旋转运动90°(运动至最高点)时,△AOP的AO边上的高取得最大值,此时△AOP的面积取得最大值,
∴t=90÷15=6秒,
∴当t=6秒时,四边形OMPN面积最大.
此时,PQ与半圆O相切.理由如下:
∵此时∠POB=90°,PQ//OB,
∴∠OPQ=90°,
∴PQ与半圆O相切;
②当点Q在半圆O上时,
∵四边形POBQ为平行四边形,且OB=OP,
∴四边形POBQ为菱形,
∴OB=BQ=OQ=OP=PQ,
∴∠POQ=∠BOQ=60°,即:∠BOP=120°,
∴此时,t=120°÷15°=8秒,
当点P与点A重合时,t=180°÷15°=12秒,
综上所述:当8<t<12时,点Q在半圆O内.




科目:初中数学 来源: 题型:
【题目】甲、乙两个草莓采摘园为吸引顾客,在草莓销售价格相同的基础上分别推出优惠方案,甲园:顾客进园需购买门票,采摘的草莓按六折优惠.乙园:顾客进园免门票,采摘草莓超过一定数量后,超过的部分打折销售.活动期间,某顾客的草莓采摘量为x kg,若在甲园采摘需总费用y1元,若在乙园采摘需总费用y2元, y1,y2与x之间的函数图象如图所示,则下列说法中错误的是( )
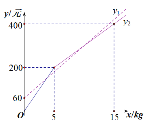
A.甲园的门票费用是60元
B.草莓优惠前的销售价格是40元/kg
C.乙园超过5 kg后,超过的部分价格优惠是打五折
D.若顾客采摘12 kg草莓,那么到甲园或乙园的总费用相同
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,以
中,以![]() 为直径的
为直径的![]() ,交
,交![]() 于点
于点![]() ,且
,且![]() 交直线
交直线![]() 于点
于点![]() ,连接
,连接![]() .
.
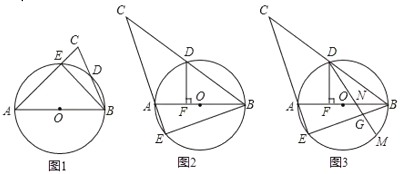
![]() 如图1,求证:
如图1,求证:![]() ;
;
![]() 如图2,
如图2,![]() 为钝角时,过点
为钝角时,过点![]() 作
作![]() 于点
于点![]() 求证:
求证:![]() ;
;
![]() 如图3,在
如图3,在![]() 的条件下,在∠BDF的内部作
的条件下,在∠BDF的内部作![]() ,使
,使![]() 分别交
分别交![]() 于点
于点![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
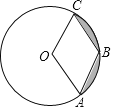
【题目】如图,已知⊙O的半径是2,点A、B、C在⊙O上,若四边形OABC为菱形,则图中阴影部分面积为( )
A. ![]() π﹣2
π﹣2![]() B.
B. ![]() π﹣
π﹣![]() C.
C. ![]() π﹣2
π﹣2![]() D.
D. ![]() π﹣
π﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=x+4的图象与反比例函数y=![]() (k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求此反比例函数的表达式;
(2)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标.
S△BOC,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七巧板是我国祖先的一项卓越创造,如图正方形ABCD可以制作一副七巧板,现将这副七巧板拼成如图2的“风车”造型(内部有一块空心),连结最外围的风车顶点M、N、P、Q得到一个四边形MNPQ,则正方形ABCD与四边形MNPQ的面积之比为( )
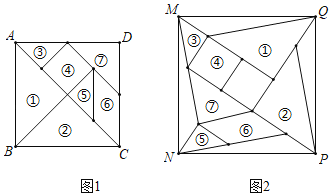
A.5:8B.3:5C.8:13D.25:49
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,Rt△ABC中,点D,E分别为直角边AC,BC上的点,若满足AD2+BE2=DE2,则称DE为R△ABC的“完美分割线”.显然,当DE为△ABC的中位线时,DE是△ABC的一条完美分割线.
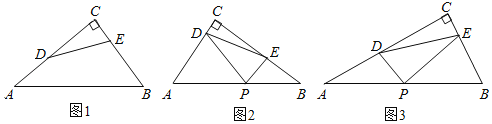
(1)如图1,AB=10,cosA=![]() ,AD=3,若DE为完美分割线,则BE的长是 .
,AD=3,若DE为完美分割线,则BE的长是 .
(2)如图2,对AC边上的点D,在Rt△ABC中的斜边AB上取点P,使得DP=DA,过点P画PE⊥PD交BC于点E,连结DE,求证:DE是直角△ABC的完美分割线.
(3)如图3,在Rt△ABC中,AC=10,BC=5,DE是其完美分割线,点P是斜边AB的中点,连结PD、PE,求cos∠PDE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学初三年级积极推进走班制教学.为了了解一段时间以来,“至善班”的学习效 果,年级组织了多次定时测试,现随机选取甲、乙两个“至善班”,从中各抽取![]() 名同学在某一次定时测试中的数学成绩,其结果记录如下:
名同学在某一次定时测试中的数学成绩,其结果记录如下:
收集数据:
“至善班”甲班![]() 的名同学的数学成绩统计(满分为 100 分)(单位:分)
的名同学的数学成绩统计(满分为 100 分)(单位:分)
![]()
![]()
“至善班”乙班的![]() 名同学的数学成绩统计(满分为 100 分)(单位:分)
名同学的数学成绩统计(满分为 100 分)(单位:分)
![]()
![]()
整理数据:(成绩得分用![]() 表示)
表示)
分数 数量 班级 |
|
|
|
|
|
甲班(人数) | 1 | 3 | 4 | 6 | 6 |
乙班(人数) | 1 | 1 | 8 | 6 | 4 |
分析数据,并回答下列问题:
![]() 完成下表:
完成下表:
平均数 | 中位数 | 众数 | |
甲班 |
|
|
|
乙班 |
|
|
|
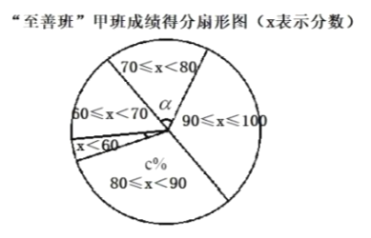
![]() 在“至善班”甲班的扇形图中, 成绩在
在“至善班”甲班的扇形图中, 成绩在![]() 的扇形中,所对的圆心角
的扇形中,所对的圆心角![]() 的度数为 . 估计全部“至善班”的
的度数为 . 估计全部“至善班”的![]() 人中优秀人数为 人.(
人中优秀人数为 人.(![]() 分及以上为优秀).
分及以上为优秀).
![]() 根据以上数据,你认为“至善班” 班(填“甲”或“乙”)所选取做样本 的同学的学习效果更好一些,你所做判断的理由是:
根据以上数据,你认为“至善班” 班(填“甲”或“乙”)所选取做样本 的同学的学习效果更好一些,你所做判断的理由是:
①
②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,⊙O的半径为r(r>0).给出如下定义:若平面上一点P到圆心O的距离d,满足![]() ,则称点P为⊙O的“随心点”.
,则称点P为⊙O的“随心点”.

(1)当⊙O的半径r=2时,A(3,0),B(0,4),C(﹣![]() ,2),D(
,2),D(![]() ,﹣
,﹣![]() )中,⊙O的“随心点”是_____;
)中,⊙O的“随心点”是_____;
(2)若点E(4,3)是⊙O的“随心点”,求⊙O的半径r的取值范围;
(3)当⊙O的半径r=2时,直线y=x+b(b≠0)与x轴交于点M,与y轴交于点N,若线段MN上存在⊙O的“随心点”,直接写出b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com