
【题目】如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,则△PMN周长的最小值是_______.

【答案】9
【解析】
要求PM+PN的最小值,PM、PN不能直接求,可考虑通过作辅助线转化PN、PM的值,从而找出其最小值,即可求出△PMN周长的最小值.
解:如图:连接MN,作ME⊥AC交AD于E,连接EN,
则EN就是PM+PN的最小值,
∵菱形ABCD,M、N分别是AB、BC的中点,
∴BN=BM=AM,MN=![]()
∵ME⊥AC交AD于E,
∴AE=AM,
∴AE=BN,AE∥BN,
∴四边形ABNE是平行四边形,
∴EN=AB,EN∥AB,
而由题意可知,可得AB=![]() =5,
=5,
∴EN=AB=5,
∴PM+PN的最小值为5.
∵MN不变,当PM+PN的最小值时,△PMN周长最小 ,
∴△PMN周长最小=9
故答案为:9.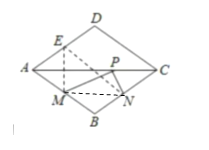


科目:初中数学 来源: 题型:
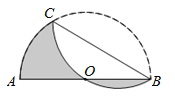
【题目】如图,AB是半圆O的直径,且AB=6cm,点C为半圆上的一点,将此半圆沿BC所在的直线折叠,若圆弧BC恰好过圆心O,则图中阴影部分的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C:y=ax2﹣2ax+3开口向下.
(1)当抛物线C过点(1,4)时,求a的值和抛物线与y轴的交点坐标;
(2)求二次函数y=ax2﹣2ax+3的对称轴和最大值(用含a的式子表示);
(3)将抛物线C向左平移a个单位得到抛物线C1,随着a的变化,抛物线C1顶点的纵坐标y与横坐标x之间存在一个函数关系,求这个函数关系式,并写出自变量x的取值范围;
(4)记(3)所求的函数为D,抛物线C与函数D的图象交于点M,结合图象,请直接写出点M的纵坐标的取值范围.
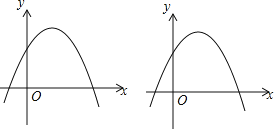
查看答案和解析>>
科目:初中数学 来源: 题型:
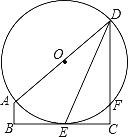
【题目】如图,在直角梯形ABCD中,AB∥CD,∠C=90°,以AD为直径的⊙O与BC相切于点E,交CD于点F,连接DE.
(1)证明:DE平分∠ADC;
(2)已知AD=4,设CD的长为x(2<x<4).
①当x=2.5时,求弦DE的长度;
②当x为何值时,DFFC的值最大?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
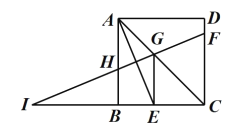
【题目】如图,在正方形![]() 中,
中,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() 垂直平分线段
垂直平分线段 ![]() ,分别交
,分别交![]() 、
、 ![]() 、
、![]() 延长线于点
延长线于点![]() 、
、![]() 、
、![]() ,则下列结论: ①
,则下列结论: ①![]() ; ②
; ② ![]() ; ③
; ③ ![]() ; ④
; ④ ![]() .其中正确的结论是__________.(填写所有正确结论的序号)
.其中正确的结论是__________.(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,草原上有A,B,C三个互通公路的奶牛养殖基地,B与C之间距离为100千米,C在B的正北方,A在C的南偏东60°方向且在B的北偏东30°方向.A地每年产奶3万吨;B地有奶牛9000头,平均每头牛的年产奶量为3吨;C地养了三种奶牛,其中黑白花牛的头数占20%,三河牛的头数占35%,其他情况反映在图(2),图(3)中.

(1)通过计算补全图(3);
(2)比较B地与C地中,哪一地平均每头牛的年产奶量更高?
(3)如果从B,C两地中选择一处建设一座工厂解决三个基地的牛奶加工问题,当运送一吨牛奶每千米的费用都为1元,那么从节省运费的角度考虑,应在何处建设工厂?
查看答案和解析>>
科目:初中数学 来源: 题型:
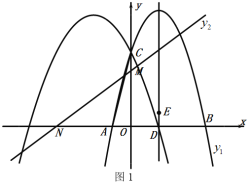
【题目】如图1,抛物线![]() 与抛物线
与抛物线![]() 相交y轴于点C,抛物线
相交y轴于点C,抛物线![]() 与x轴交于A、B两点(点B在点A的右侧),直线
与x轴交于A、B两点(点B在点A的右侧),直线![]() 交x轴负半轴于点N,交y轴于点M,且
交x轴负半轴于点N,交y轴于点M,且![]() .
.
(1)求抛物线![]() 的解析式与k的值;
的解析式与k的值;
(2)抛物线![]() 的对称轴交x轴于点D,连接
的对称轴交x轴于点D,连接![]() ,在x轴上方的对称轴上找一点E,使以点A,D,E为顶点的三角形与
,在x轴上方的对称轴上找一点E,使以点A,D,E为顶点的三角形与![]() 相似,求出
相似,求出![]() 的长;
的长;
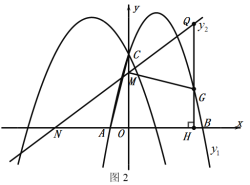
(3)如图2,过抛物线![]() 上的动点G作
上的动点G作![]() 轴于点H,交直线
轴于点H,交直线![]() 于点Q,若点
于点Q,若点![]() 是点Q关于直线
是点Q关于直线![]() 的对称点,是否存在点G(不与点C重合),使点
的对称点,是否存在点G(不与点C重合),使点![]() 落在y轴上?若存在,请直接写出点G的横坐标,若不存在,请说明理由.
落在y轴上?若存在,请直接写出点G的横坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,全球疫情大爆发,我国派遣医疗专家组对一些国家进行医疗援助,某批次派出20人组成的专家组,分别赴A、B、C、D四个国家开展援助工作,七人员分布情况如统计图(不完整)所示:
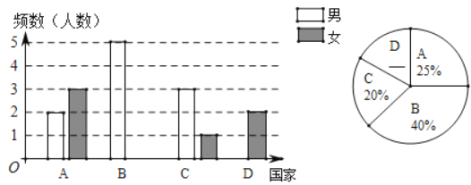
(1)计算赴B国女专家和D国男专家的人数,并将条形统计图补充完整;
(2)根据需要,从赴A国的专家,随机抽取两名专家对当地医疗团队进行培训,求所抽取的两名专家恰好是一男一女的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com