
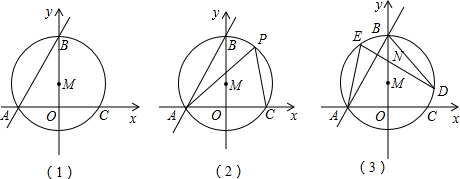
���� ��1����ͼ��1����ʾ������M��MD��AB������ΪD������õ�A��B�����꣬�Ӷ��õ�OA=2$\sqrt{3}$��OB=6����������������Ǻ���ֵ����á�ABO=30�㣬���ǵõ�AB=2AO=4$\sqrt{3}$���ɴ���������֪DB=AD=2$\sqrt{3}$��Ȼ���١�DBM�У�������������Ǻ���ֵ�����MB=4���Ӷ�����õ�M�����ꣻ
��2����ͼ��2����ʾ������BC����AP��ȡ��NʹPB=PN����֤����BPN�ǵȱ������Σ�Ȼ����֤����ANB�ա�CPB���Ӷ��ɵõ�PB+PC=PA��
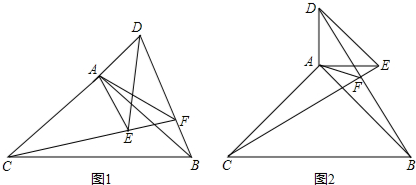
��3����ͼ��3����ʾ���ӳ�AM����M�ڵ�F������BF��EF��CG����֤��ED��BF�����ǵõ�$\widehat{BE}=\widehat{FD}$��Ȼ��֤��$\widehat{EF}=\widehat{BD}$���ʴˡ�EAF=��BGD�����EAF=��BGD=������������Ǻ����Ķ����֪��AE=AF•cos��=2rcos����BD=GBsin��=2rsin������sina2+cosa2=1��֪��AE2+BD2=4r2��rΪ��M�İ뾶����
��� �⣺��1����ͼ��1����ʾ������M��MD��AB������ΪD��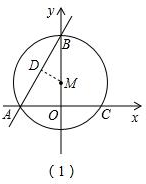
��x=0�ã�y=6��
���B��������0��6����
��y=0�ã�$\sqrt{3}$x+6=0��
��ã�x=-2$\sqrt{3}$��
��OA=2$\sqrt{3}$��
��tan��ABO=$\frac{2\sqrt{3}}{6}$=$\frac{\sqrt{3}}{3}$��
���ABO=30�㣮
��Rt��AOB��AB=$\sqrt{A{O}^{2}+O{B}^{2}}$=4$\sqrt{3}$��
��MD��AB��
��DA=DB=2$\sqrt{3}$��
��$\frac{BD}{MB}=\frac{\sqrt{3}}{2}$����$\frac{2\sqrt{3}}{MB}=\frac{\sqrt{3}}{2}$��
��ã�MB=4��
��OM=OB-BM=2��
���M��������0��2����
��2����ͼ��2����ʾ������BC����AP��ȡ��NʹPB=PN��
��MO��AC��
��OC=OA=2$\sqrt{3}$��
��tan��BCO=$\frac{6}{2\sqrt{3}}$=$\sqrt{3}$��
���BCO=60�㣮
���BPA=60�㣮
�֡�PB=PN��
���BPN�ǵȱ������Σ�
���BNP=60�㣬��BPN=60�㣬BN=BP��
���ANB=120�㣮
�ڡ�ABC�С�BAC=��BCA=60�㣬
���ABC=60�㣮
���APC=60�㣮
���BPC=��BPN+��APC=120�㣮
���ANB=��CPB��
�ڡ�ANB�͡�CPB��$\left\{\begin{array}{l}{��BAN=��BCP}\\{��ANB=��CPB}\\{BN=BP}\end{array}\right.$��
���ANB�ա�CPB��
��AN=PC��
��AP=AN+PN=PC+PB��
��PB+PC=PA��
��3��AE2+BD2��ֵ���䣮
���ɣ���ͼ��3����ʾ���ӳ�AM����M�ڵ�F������BF��EF��CG��
��AF�ǡ�M��ֱ����
���AEF=��ABF=90�㣮
��BF��AB��
��ED��AB��
��ED��BF��
��$\widehat{BE}=\widehat{FD}$��
��$\widehat{EF}=\widehat{BD}$��
���EAF=��BGD��
���EAF=��BGD=������AE=AF•cos��=2rcos����BD=GBsin��=2rsin����rΪ��M�İ뾶����
��AE2+BD2=��2rcos����2+��2rsin����2=4r2��sina2+cosa2��=4r2��
���� ������Ҫ�������Բ�����ʡ�һ�κ���������������Ǻ���ֵ��������Ǻ����Ķ��塢�ȱ������ε����ʺ��ж���ȫ�������ε����ʺ��ж������ձ���ĸ����ߵ������ǽ����Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ������y=x2+bx+c��x�ύ��A��-1��0����B��3��0����y�ύ�ڵ�C�������ߵĶԳ��ύx���ڵ�D��P��ֱ��BC��һ���㣮
������y=x2+bx+c��x�ύ��A��-1��0����B��3��0����y�ύ�ڵ�C�������ߵĶԳ��ύx���ڵ�D��P��ֱ��BC��һ���㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
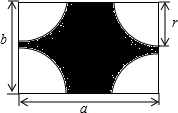 ��ͼ����һ�鳤Ϊa�ף���Ϊb�ij�������Ƥ�����ĸ��Ƿֱ��ȥ�뾶����r���ķ�֮һ��Բ�Σ�
��ͼ����һ�鳤Ϊa�ף���Ϊb�ij�������Ƥ�����ĸ��Ƿֱ��ȥ�뾶����r���ķ�֮һ��Բ�Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com