
【题目】已知等边△ABC和⊙M.
(1)如图l,若⊙M与BA的延长线AK及边AC均相切,求证: AM∥BC;
(2)如图2,若⊙M与BA的延长线AK、BC的延长线CF及边AC均相切,求证:四边形ABCM是平行四边形.

【答案】证明见解析
【解析】证明:(1)连接AM,

∵△ABC是等边三角形,∴∠B=∠BAC=60°。
∴∠KAC=180°﹣∠BAC=120°。
∵⊙M与BA的延长线AK及边AC均相切,
∴∠KAM=∠CAM=![]() ∠KAC=
∠KAC=![]() ×120°=60°。
×120°=60°。
∴∠KAM=∠B=60°。∴AM∥BC。
(2)∵△ABC是等边三角形,∴∠B=∠BAC=∠ACB=60°。
∴∠KAC=180°﹣∠BAC=120°,∠FCA=120°。
∵⊙M与BA的延长线AK、BC的延长线CF及边AC均相切,
∴∠KAM=∠CAM=![]() ∠KAC=
∠KAC=![]() ×120°=60°,
×120°=60°,
∠FCM=∠ACM=![]() ∠FCA=
∠FCA=![]() ×120°=60°。
×120°=60°。
∴∠KAM=∠B=60°,∠FCM=∠B=60°。
∴AM∥BC,CM∥AB,∴四边形ABCM是平行四边形。
(1)由等边△ABC,即可得∠B=∠BAC=60°,求得∠KAC=120°,又由⊙M与BA的延长线AK及边AC均相切,利用切线长定理,即可得∠KAM=60°,然后根据同位角相等,两直线平行,证得AM∥BC。
(2)根据(1),易证得AM∥BC,CM∥AB,从而可证得四边形ABCM是平行四边形。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】①如图1,AB∥CD,则∠A +∠E +∠C=180°;②如图2,AB∥CD,则∠E =∠A +∠C;③如图3,AB∥CD,则∠A +∠E-∠1=180° ; ④如图4,AB∥CD,则∠A=∠C +∠P.以上结论正确的个数是( )



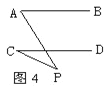
A. 、1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,各内角的平分线分别相交于点E,F,G,H.
(1)求证:△ABG≌△CDE;
(2)猜一猜:四边形EFGH是什么样的特殊四边形?证明你的猜想;
(3)若AB=6,BC=4,∠DAB=60°,求四边形EFGH的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业今年8月的产值为a万元, 9月份比8月份增加了10%,10月份比9月份增加了15%,则10月份的产值是( )
A.a(1 10%)(1 15%)万元B.(a 10%)(a 15%)万元
C.a(1 90%)(1 85%)万元D.a(1 10% 15%)万元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com