

分析 (1)设抛物线的表达式为y=a(x-2)2,然后将(0,1)代入可求得a的值,从而可求得二次函数的表达式;
(2)根据两点间的距离公式可求圆的半径,再根据两点间的距离公式可求点M、N的坐标;
(3)过点C作CH⊥x轴,垂足为H,连接BC、CN,由勾股定理可知HC2=CN2-CH2=BC2-CH2,依据两点间的距离公式可求得HN=2,结合垂径定理可求得MN的长;
解答 解:(1)设抛物线的表达式为y=a(x-2)2.
∵将(0,1)代入得:4a=1,解得a=$\frac{1}{4}$,
∴抛物线的解析式为y=$\frac{1}{4}$(x-2)2.
(2)AB=$\sqrt{(2-2)^{2}+(2-0)^{2}}$=2,
M的坐标为(2-2,0),即(0,0),
N的坐标为(2+2,0),即(4,0);
(3)MN的长不发生变化.
理由:如图所示,过点C作CH⊥x轴,垂足为H,连接BC、CN.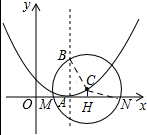
设点C的坐标为(a,$\frac{1}{4}$(a-2)2).
∵CH⊥MN,
∴MH=HN.
∵HN2=CN2-CH2=CB2-CH2,
∴HN2=[2-$\frac{1}{4}$(a-2)2]2+(a-2)2-[$\frac{1}{4}$(a-2)2]2=4.
∴HN=2.
∴MN=4.
∴MN不发生变化.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数函数的解析式、垂径定理、两点间的距离公式、勾股定理,综合性较强,难度中等.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示格点图中,每个小正方形的边长均为1,△ABC的三个顶点均在格点上,以原点O为位似中心,相似比为$\frac{1}{2}$,把△ABC缩小,则点C的对应点C′的坐标为( )
如图所示格点图中,每个小正方形的边长均为1,△ABC的三个顶点均在格点上,以原点O为位似中心,相似比为$\frac{1}{2}$,把△ABC缩小,则点C的对应点C′的坐标为( )| A. | (1,$\frac{3}{2}$) | B. | (2,6) | C. | (2,6)或(-2,-6) | D. | (1,$\frac{3}{2}$)或(-1,-$\frac{3}{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
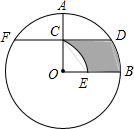 如图,在⊙O中,半径OA⊥OB,过点OA的中点C作FD∥OB交⊙O于D、F两点,且CD=$\sqrt{3}$,以O为圆心,OC为半径作$\widehat{CE}$,交OB于E点.
如图,在⊙O中,半径OA⊥OB,过点OA的中点C作FD∥OB交⊙O于D、F两点,且CD=$\sqrt{3}$,以O为圆心,OC为半径作$\widehat{CE}$,交OB于E点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
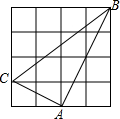 如图,在4×4的正方形网格图中有△ABC,则sin∠ABC=( )
如图,在4×4的正方形网格图中有△ABC,则sin∠ABC=( )| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>2 | B. | m<3 | C. | 2<m<3 | D. | m>3或m<2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=-1}\\{y=-3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-\frac{7}{5}}\\{y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2}\\{y=-\frac{3}{2}}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
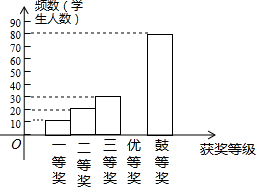 国务院办公厅2015年3月16日发布了《中国足球改革的总体方案》,这是中国足球历史上的重大改革.为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
国务院办公厅2015年3月16日发布了《中国足球改革的总体方案》,这是中国足球历史上的重大改革.为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:| 获奖等次 | 频数 | 频率 |
| 一等奖 | 10 | 0.05 |
| 二等奖 | 20 | 0.10 |
| 三等奖 | 30 | b |
| 优胜奖 | a | 0.30 |
| 鼓励奖 | 80 | 0.40 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com