
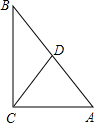
 实验探究:要把两直角边分别是30米和40米的Rt△ABC菜地分成面积相等的两块,分给两菜农,且使分割线段尽量短.
实验探究:要把两直角边分别是30米和40米的Rt△ABC菜地分成面积相等的两块,分给两菜农,且使分割线段尽量短.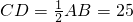 (米).
(米).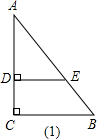 解:(1)根据相似三角形面积比是相似比的平方,我们可以过直角边40米上一点,作平行于另一直角边的直线,将三角形分成两部分,面积相等,边长比为,1:(
解:(1)根据相似三角形面积比是相似比的平方,我们可以过直角边40米上一点,作平行于另一直角边的直线,将三角形分成两部分,面积相等,边长比为,1:( -1),
-1), 和40-20
和40-20 ,
, ≈21.2米<25米.
≈21.2米<25米.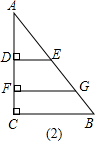
 -1):(
-1):( -
- ),
), -1)两部分,即可解决.(2)同理,在直角边上找两点,分成1:(
-1)两部分,即可解决.(2)同理,在直角边上找两点,分成1:( ):(
):( ),即可解决.
),即可解决.

 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
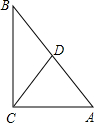 实验探究:要把两直角边分别是30米和40米的Rt△ABC菜地分成面积相等的两块,分给两菜农,且使分割线段尽量短.
实验探究:要把两直角边分别是30米和40米的Rt△ABC菜地分成面积相等的两块,分给两菜农,且使分割线段尽量短.| 1 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com