
【题目】如图,抛物线y=ax2+2ax+1与x轴仅有一个公共点A,经过点A的直线交该抛物线于点B,交y轴于点C,且点C是线段AB的中点.
(1)求这条抛物线对应的函数解析式;
(2)求直线AB对应的函数解析式.
【答案】
(1)
解:∵抛物线y=ax2+2ax+1与x轴仅有一个公共点A,
∴△=4a2﹣4a=0,解得a1=0(舍去),a2=1,
∴抛物线解析式为y=x2+2x+1;
(2)
解:∵y=(x+1)2,
∴顶点A的坐标为(﹣1,0),
∵点C是线段AB的中点,
即点A与点B关于C点对称,
∴B点的横坐标为1,
当x=1时,y=x2+2x+1=1+2+1=4,则B(1,4),
设直线AB的解析式为y=kx+b,
把A(﹣1,0),B(1,4)代入得 ![]() ,解得
,解得 ![]() ,
,
∴直线AB的解析式为y=2x+2
【解析】(1)利用△=b2﹣4ac=0时,抛物线与x轴有1个交点得到4a2﹣4a=0,然后解关于a的方程求出a,即可得到抛物线解析式;(2)利用点C是线段AB的中点可判断点A与点B的横坐标互为相反数,则可以利用抛物线解析式确定B点坐标,然后利用待定系数法求直线AB的解析式.本题考查了抛物线与x轴的交点:对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),△=b2﹣4ac决定抛物线与x轴的交点个数:△=b2﹣4ac>0时,抛物线与x轴有2个交点;△=b2﹣4ac=0时,抛物线与x轴有1个交点;△=b2﹣4ac<0时,抛物线与x轴没有交点.也考查了利用待定系数法求函数解析式.
【考点精析】利用确定一次函数的表达式和抛物线与坐标轴的交点对题目进行判断即可得到答案,需要熟知确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】为深化义务教育课程改革,某校积极开展拓展性课程建设,计划开设艺术、体育、劳技、文学等多个类别的拓展性课程,要求每一位学生都自主选择一个类别的拓展性课程.为了了解学生选择拓展性课程的情况,随机抽取了部分学生进行调查,并将调查结果绘制成如下统计图(部分信息未给出):
根据统计图中的信息,解答下列问题:
(1)求本次被调查的学生人数.
(2)将条形统计图补充完整.
(3)若该校共有1600名学生,请估计全校选择体育类的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.(写出一种即可)
关系:①AD∥BC,②AB=CD,③∠A=∠C,④∠B+∠C=180°.
已知:在四边形ABCD中, , ;
求证:四边形ABCD是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】希望中学计划从荣威公司买A、B两种型号的小黑板,经治谈,购买一块A型小黑板比购买一块B型小黑板多用20元,且购买5块A型小黑板和购买4块B型小黑板共需820元.
![]() 求购买一块A型小黑板,一块B型小黑板各需要多少元?
求购买一块A型小黑板,一块B型小黑板各需要多少元?
![]() 根据希望中学实际情况,需从荣威公司买A,B两种型号的小黑板共60块,要求购买A、B两种型号的小黑板的总费用不超过5240元,并且购买A型小黑板的数量应大于购买A、B两种型号的小黑板总数量的
根据希望中学实际情况,需从荣威公司买A,B两种型号的小黑板共60块,要求购买A、B两种型号的小黑板的总费用不超过5240元,并且购买A型小黑板的数量应大于购买A、B两种型号的小黑板总数量的![]() ,请你通过计算,求出希望中学从荣威公司买A、B两种型号的小黑板有哪几种方案?并说明哪种方案更节约资金?
,请你通过计算,求出希望中学从荣威公司买A、B两种型号的小黑板有哪几种方案?并说明哪种方案更节约资金?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )

A. △AFD≌△DCE B. AF=![]() AD C. AB=AF D. BE=AD﹣DF
AD C. AB=AF D. BE=AD﹣DF
查看答案和解析>>
科目:初中数学 来源: 题型:
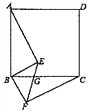
【题目】如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G.
(1)求证:AE=CF;
(2)若∠ABE=55°,求∠EGC的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料;
课堂上,老师设计了一个活动:将一个4×4的正方形网格沿着网格线划分成两部分(分别用阴影和空白表示),使得这两部分图形是全等的,请同学们尝试给出划分的方法.约定:如果两位同学的划分结果经过旋转、翻折后能够重合,那么就认为他们的划分方法相同.
小方、小易和小红分别对网格进行了划分,结果如图①、图②、图③所示.
小方说:“我们三个人的划分方法都是正确的,但是将小红的整个图形(图③)逆时针旋转90![]() 后得到的划分方法与我的划分方法(图①)是一样的,应该认为是同一种方法,而小易的划分方法与我的不同,”
后得到的划分方法与我的划分方法(图①)是一样的,应该认为是同一种方法,而小易的划分方法与我的不同,”
老师说:“小方说得对.”

完成下列问题:
(1)图④的划分方法是否正确?
(2)判断图⑤的划分方法与图②小易的划分方法是否相同,并说明你的理由.
(3)请你再想出一种与已有方法不同的划分方法,使之满足上述条件,并在图⑥中画出来.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,把一条抛物线先向上平移3个单位长度,然后绕原点选择180°得到抛物线y=x2+5x+6,则原抛物线的解析式是( )
A.y=﹣(x﹣ ![]() )2﹣
)2﹣ ![]()
B.y=﹣(x+ ![]() )2﹣
)2﹣ ![]()
C.y=﹣(x﹣ ![]() )2﹣
)2﹣ ![]()
D.y=﹣(x+ ![]() )2+
)2+ ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com