
 如图,要测量河两岸相对的两点A、B的距离,先过点B作BF⊥AB,在BF上找点D,过D作DE⊥BF,再取BD的中点C,连接AC并延长,与DE交点为E,此时测得DE的长度就是AB的长度.这里判定△ABC和△EDC全等的依据是( )
如图,要测量河两岸相对的两点A、B的距离,先过点B作BF⊥AB,在BF上找点D,过D作DE⊥BF,再取BD的中点C,连接AC并延长,与DE交点为E,此时测得DE的长度就是AB的长度.这里判定△ABC和△EDC全等的依据是( )| A. | ASA | B. | SAS | C. | SSS | D. | AAS |
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:选择题
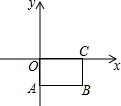 已知,矩形OABC按如图所示的方式建立在平面直角坐标系总,AB=4,BC=2,则点B的坐标为( )
已知,矩形OABC按如图所示的方式建立在平面直角坐标系总,AB=4,BC=2,则点B的坐标为( )| A. | (4,2) | B. | (-2,4) | C. | (4,-2) | D. | (-4,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>$\frac{1}{5}$ | B. | m<$\frac{1}{5}$ | C. | m≥$\frac{1}{5}$ | D. | m≤$\frac{1}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=-x-2 | B. | y=-x-6 | C. | y=-x-10 | D. | y=-x-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
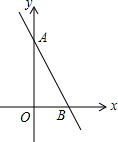 如图,若一次函数y=-2x+b的图象交y轴于点A(0,3),则不等式-2x+b>0的解集为( )
如图,若一次函数y=-2x+b的图象交y轴于点A(0,3),则不等式-2x+b>0的解集为( )| A. | x>$\frac{3}{2}$ | B. | x>3 | C. | x<$\frac{3}{2}$ | D. | x<3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com