
【题目】如图,一块等腰三角形钢板的底边长为![]() ,腰长为
,腰长为![]() .
.
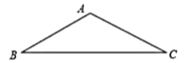
(1)求能从这块钢板上截得的最大圆的半径;
(2)用一个圆完整覆盖这块钢板,这个圆的最小半径是多少![]() ?
?
【答案】(1)![]() cm;(2)40cm.
cm;(2)40cm.
【解析】
(1)由于三角形ABC是等腰三角形,过A作AD⊥BC于D,那么根据勾股定理得到AD=30,又从这块钢板上截得的最大圆就是三角形的内切圆,根据内切圆的圆心的性质知道其圆心在AD上,分别连接AO、BO、CO,然后利用三角形的面积公式即可求解;
(2)由于一个圆完整覆盖这块钢板,那么这个圆是三个三角形的外接圆,设覆盖圆的半径为R,根据垂径定理和勾股定理即可求解
解:(1)如图,过A作AD⊥BC于D

∵AB=AC=50,BC=80
∴根据等腰三角形三线合一的性质及勾股定理可得
AD=30,BD=CD=40,
设最大圆半径为r,
则S△ABC=S△ABO+S△BOC+S△AOC,
∴S△ABC=![]() ×BC×AD=
×BC×AD=![]() (AB+BC+CA)r
(AB+BC+CA)r
![]() ×80×30=
×80×30=![]() (50+80+50)r
(50+80+50)r
解得:r=![]() cm ;
cm ;
(2)设覆盖圆的半径为R,圆心为O′,

∵△ABC是等腰三角形,过A作AD⊥BC于D,
∴BD=CD=40,AD=![]() ,
,
∴O′在AD直线上,连接O′C,
在Rt△O′DC中,
由R2=402+(R-30)2,
∴R=![]() ;
;
若以BD长为半径为40cm,也可以覆盖,
∴最小为40cm.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
【题目】某校3男2女共5名学生参加黄石市教育局举办的“我爱黄石”演讲比赛.
(1)若从5名学生中任意抽取3名,共有多少种不同的抽法,列出所有可能情形;
(2)若抽取的3名学生中,某男生抽中,且必有1女生的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
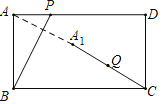
【题目】如图在矩形ABCD中,AB=![]() ,AD=3,点P是AD边上的一个动点,连接BP,作点A关于直线BP的对称点A1,连接A1C,设A1C的中点为Q,当点P从点A出发,沿边AD运动到点D时停止运动,点Q的运动路径长为( )
,AD=3,点P是AD边上的一个动点,连接BP,作点A关于直线BP的对称点A1,连接A1C,设A1C的中点为Q,当点P从点A出发,沿边AD运动到点D时停止运动,点Q的运动路径长为( )
A.![]() πB.
πB.![]() πC.
πC.![]() πD.π
πD.π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大型商场出售一种时令鞋,每双进价100元,售价300元,则每月能售出400双.经市场调查发现:每降价10元,则每天可多售出50双.设每双降价x元,每天总获利y元.
(1)如果降价40元,每天总获利多少元呢?
(2)每双售价为多少元时,每天的总获利最大?最大获利是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
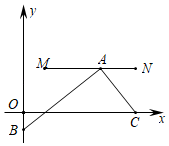
【题目】如图,在平面直角坐标系中,M、N、C三点的坐标分别为(![]() ,1),(3,1),(3,0),点A为线段MN上的一个动点,连接AC,过点A作AB⊥AC交y轴于点B,当点A从M运动到N时,点B随之运动,设点B的坐标为(0,b),则b的取值范围是( )
,1),(3,1),(3,0),点A为线段MN上的一个动点,连接AC,过点A作AB⊥AC交y轴于点B,当点A从M运动到N时,点B随之运动,设点B的坐标为(0,b),则b的取值范围是( )
A.![]() ≤b≤1B.
≤b≤1B.![]() ≤b≤1C.
≤b≤1C.![]() ≤b≤
≤b≤![]() D.
D.![]() ≤b≤1
≤b≤1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段![]() ,
,![]() 于点
于点![]() ,且
,且![]() ,
,![]() 是射线
是射线![]() 上一动点,
上一动点,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,过点
的中点,过点![]() ,
,![]() ,
,![]() 的圆与
的圆与![]() 的另一交点
的另一交点![]() (点
(点![]() 在线段
在线段![]() 上),连结
上),连结![]() ,
,![]() .
.
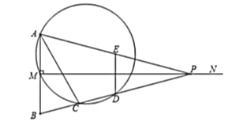
(1)当![]() 时,求
时,求![]() 的度数;
的度数;
(2)求证:![]() ;
;
(3)在点![]() 的运动过程中,当
的运动过程中,当![]() 时,取四边形
时,取四边形![]() 一边的两端点和线段
一边的两端点和线段![]() 上一点
上一点![]() ,若以这三点为顶点的三角形是直角三角形,且
,若以这三点为顶点的三角形是直角三角形,且![]() 为锐角顶点,求所有满足条件的
为锐角顶点,求所有满足条件的![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
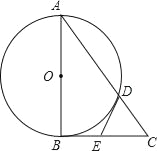
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,点E为BC的中点,连接DE.
(1)求证:DE是⊙O的切线;
(2)求证:4DE2=CDAC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学测试中,同年级人数相同的甲、乙两个班的成绩统计如下表:
班级 | 平均分 | 中位数 | 方差 |
甲班 |
|
|
|
乙班 |
|
|
|
数学老师让同学们针对统计的结果进行一下评估,学生的评估结果如下:
![]() 这次数学测试成绩中,甲、乙两个班的平均水平相同;
这次数学测试成绩中,甲、乙两个班的平均水平相同;
![]() 甲班学生中数学成绩95分及以上的人数少;
甲班学生中数学成绩95分及以上的人数少;
![]() 乙班学生的数学成绩比较整齐,分化较小.
乙班学生的数学成绩比较整齐,分化较小.
上述评估中,正确的是______![]() 填序号
填序号![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒子里有标号分别为1,2,3,4的四个球,这些球除标号数字外都相同.
(1)从盒中随机摸出一个小球,求摸到标号数字为奇数的球的概率;
(2)甲、乙两人用这四个小球玩摸球游戏,规则是:甲从盒中随机摸出一个小球,记下标号数字后放回盒里,充分摇匀后,乙再从盒中随机摸出一个小球,并记下标号数字.若两次摸到球的标号数字同为奇数或同为偶数,则判甲赢;若两次摸到球的标号数字为一奇一偶,则判乙赢.请用列表法或画树状图的方法说明这个游戏对甲、乙两人是否公平.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com