
【题目】为了加强市民的节水意识,合理利用水资源,某市采用阶梯收费的调控手段以达到节水的目的,该市自来水收费价目表如下:
每月用水量 | 价格 | 注:水费按月结算,每户每月须缴纳5元污水处理费. |
不超出6m3的部分 | 2元/m3 | |
超出6m3不超出10m3的部分 | 3元/m3 | |
超出10m3的部分 | 5元/m3 |
若某户居民![]() 月份用水
月份用水![]() ,则应缴费
,则应缴费![]() (元),
(元),
(1)若用户![]() 月份共用水
月份共用水![]() ,则需缴费________;
,则需缴费________;
(2)若该户居民某月缴费![]() 元,则该户居民该月用水多少吨?
元,则该户居民该月用水多少吨?
【答案】(1)![]() 元;(2)该用户该月用水15吨
元;(2)该用户该月用水15吨
【解析】
(1)4月份用水9.5m3,超过6m3的部分按第二档缴费;
(2)由于6×2+(10-6)×3+5=29(元),则根据该月缴费为54元可知,用水量超过10cm3,设用水xm3,根据缴费的形式得到6×2+(10-6)×3+(x-10)×5+5=54,然后解方程即可.
解:(1)该户居民4月份用水9.5m3,应缴费=6×2+(9.5-6)×3+5=27.5(元).
故答案为:27.5元;
(2)由于6×2+(10-6)×3+5=29(元),则根据该月缴费为54元可知,用水量超过10cm3,设用水xm3,
根据题意得6×2+(10-6)×3+(x-10)×5+5=54,
解得x=15.
答:该户居民该月用水15吨.


科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AC与BD交于点O,E是BD上一点,EF//AB,∠EAB=∠EBA,过点B作DA的垂线,交DA的延长线于点G.
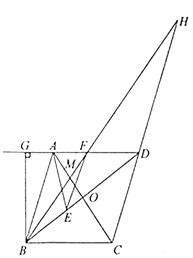
(1)∠DEF和∠AEF是否相等?若相等,请证明;若不相等,请说明理由;
(2)找出图中与ΔAGB相似的三角形,并证明;
(3)BF的延长线交CD的延长线于点H,交AC于点M.求证:BM2=MFMH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点F,D,E分别是边AB,BC,AC上的点,且AD,BE,CF相交于点O,若点O是△ABC的重心,则以下结论:①线段AD,BE,CF是△ABC的三条角平分线;②△ABD的面积是△ABC面积的一半;③图中与△ABD面积相等的三角形有5个;④△BOD的面积是△ABD面积的![]() ;⑤AO=2OD其中一定正确结论有( )
;⑤AO=2OD其中一定正确结论有( )
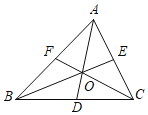
A.①③④⑤B.②③④⑤C.③④⑤D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 所在平面内一点,过点
所在平面内一点,过点![]() 分别作
分别作![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
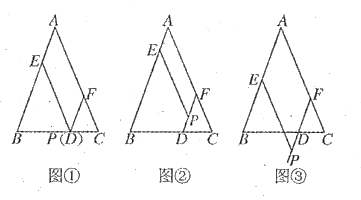
若点![]() 在
在![]() 上(如图①),此时
上(如图①),此时![]() ,可得结论:
,可得结论:![]() .
.
请应用上述信息解决下列问题:
当点![]() 分别在
分别在![]() 内(如图②),
内(如图②),![]() 外(如图③)时,上述结论是否成立?若成立,请给予证明;若不成立,
外(如图③)时,上述结论是否成立?若成立,请给予证明;若不成立,![]() ,
,![]() ,
,![]() ,与
,与![]() 之间又有怎样的数量关系,请写出你的猜想,不需要证明.
之间又有怎样的数量关系,请写出你的猜想,不需要证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊著名的毕达哥拉斯学派把1、3、6、10… 这样的数称为“三角形数”,而把1、4、9、16… 这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.则下列符合这一规律的等式是( )
![]()
![]()
 …
…
A.20=4+16B.25=9+16C.36=15+21D.49=20+29
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以直线AB上一点O为端点作射线OC,将一块直角三角板的直角顶点放在O处(注:∠DOE=90°).



(1)如图①,若直角三角板DOE的一边OD放在射线OB上,且∠BOC=60°,求∠COE的度数;
(2)如图②,将三板DOE绕O逆时针转动到某个位置时,若恰好满足5∠COD=∠AOE,且∠BOC=60°,求∠BOD的度数;
(3)如图③,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OE恰好平分∠AOC,请说明OD所在射线是∠BOC的平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC与△A′B′C′在平面直角坐标系中的位置如图.
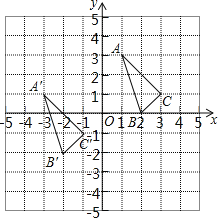
(1)分别写出下列各点的坐标: A′ ;B′ ;C′ ;
(2)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为 ;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
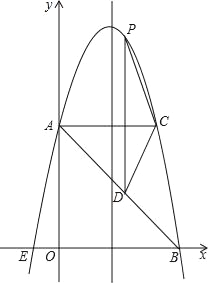
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E,B.
(1)求二次函数y=ax2+bx+c的解析式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com