
 如图,在平面直角坐标系中,直线y=-2x+2与x轴、y轴分别相交于点A、B,四边形ABCD是正方形,双曲线y=$\frac{k}{x}$ 在第一象限经过点D.
如图,在平面直角坐标系中,直线y=-2x+2与x轴、y轴分别相交于点A、B,四边形ABCD是正方形,双曲线y=$\frac{k}{x}$ 在第一象限经过点D.分析 (1)首先过点D作DE⊥x轴于点E,根据已知得出AO,BO的长度,进而得出△AOB≌△DEA,求出D点坐标,进而得出解析式;
(2)首先过点C作CF⊥y轴,利用△AOB≌△DEA,同理可得出:△AOB≌△BFC,即可得出C点纵坐标,如果点在图象上,利用纵坐标求出横坐标即可.
解答 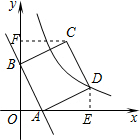 解:(1)过点D作DE⊥x轴于点E.
解:(1)过点D作DE⊥x轴于点E.
∵直线y=-2x+2与x轴,y轴相交于点A.B,
∴当x=0时,y=2,即OB=2.
当y=0时,x=1,即OA=1.
∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD.
∴∠BAO+∠DAE=90°.
∵∠ADE+∠DAE=90°,
∴∠BAO=∠ADE,
∵∠AOB=∠DEA=90°,
在△AOB和△DEA中,
$\left\{\begin{array}{l}{∠AOB=∠DEA=90°}\\{∠BAO=∠ADE}\\{AB=DA}\end{array}\right.$,
∴△AOB≌△DEA(AAS),
∴DE=AO=1,AE=BO=2,
∴OE=3,DE=1.
∴点D的坐标为(3,1)
把(3,1)代入y=$\frac{k}{x}$中,得k=3.
∴该函数解析式为:y=$\frac{3}{x}$;
(2)过点C作CF⊥y轴,
∵△AOB≌△DEA,
∴同理可得出:△AOB≌△BFC,
∴OB=CF=2,BF=OA=1,
∴点C的坐标为:(2,3),
把y=3代入y=$\frac{3}{x}$,得x=1,
即:应该将正方形ABCD沿X轴向左平移2-1=1个单位长度时,点C的对应点恰好落在(1)中的双曲线上.
故答案是:1.
点评 此题属于反比例函数的综合题,考查了待定系数求函数解析式的知识、全等三角形的判定与性质以及正方形的性质.此题难度较大,综合性较强,注意掌握辅助线的作法,注意掌握数形结合思想的应用.


科目:初中数学 来源: 题型:选择题
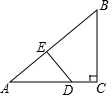 如图,在△ABC中,∠C=90°,点D、E分别在边AC、AB上.若∠B=∠ADE,则下列结论不正确的是( )
如图,在△ABC中,∠C=90°,点D、E分别在边AC、AB上.若∠B=∠ADE,则下列结论不正确的是( )| A. | ∠A和∠B互为余角 | B. | ∠A和∠ADE互为余角 | ||
| C. | ∠B和∠EDC互为补角 | D. | ∠B和∠DEB互为补角 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 解:x2-7x+10=0 a=1 b=-7 c=10 ∵b2-4ac=9>0 ∴x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{7+3}{2}$ ∴x1=5,x2=2 所以,当腰为5,底为2时,等腰三角形的三条边为5,5,2. 当腰为2,底为5时,等腰三角形的三条边为2,2,5. |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
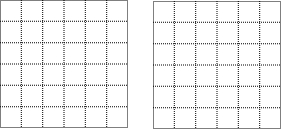 如图,正方形网络中的每个小正方形边长都为1,每个小正方形的顶点叫格点,分别按下列要求画以格点为顶点三角形和平行四边形.(无需写画法)
如图,正方形网络中的每个小正方形边长都为1,每个小正方形的顶点叫格点,分别按下列要求画以格点为顶点三角形和平行四边形.(无需写画法)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
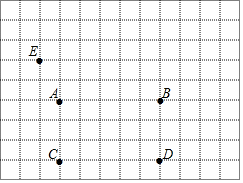 某区进行课堂教学改革,将学生分成5个学习小组,采取团团坐的方式.如图,这是某校八(1)班教室简图,点A、B、C、D、E分别代表五个学习小组的位置.已知A点的坐标为(-1,3).
某区进行课堂教学改革,将学生分成5个学习小组,采取团团坐的方式.如图,这是某校八(1)班教室简图,点A、B、C、D、E分别代表五个学习小组的位置.已知A点的坐标为(-1,3).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com