
分析 (1)①根据勾股定理分别求出两个三角形的边长,根据相似三角形的判定定理证明即可;
②根据相似三角形的性质得到∠B=∠E,等量代换即可;
(2)在CA上截取CM=CB=n,连接BM,作MN⊥AB于N,根据勾股定理求出$\frac{BM}{MN}$,证明△EFD∽△MNB,根据相似三角形的性质定理解答即可.
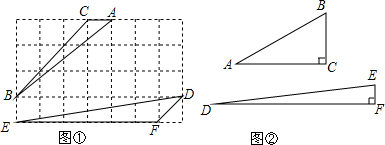
解答 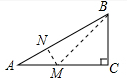 (1)①证明:AC=1,BC=3$\sqrt{2}$,AB=5,
(1)①证明:AC=1,BC=3$\sqrt{2}$,AB=5,
DF=$\sqrt{2}$,EF=6,DE=5$\sqrt{2}$,
则$\frac{AC}{DF}$=$\frac{\sqrt{2}}{2}$,$\frac{BC}{EF}$=$\frac{\sqrt{2}}{2}$,$\frac{AB}{DE}$=$\frac{\sqrt{2}}{2}$,
∴$\frac{AC}{DF}$=$\frac{BC}{EF}$=$\frac{AB}{DE}$,
∴△ABC∽△DEF;
②∵△ABC∽△DEF;
∴∠B=∠E,又∠E+∠D=45°,
∴∠B+∠D=45°;
(2)如图,在CA上截取CM=CB=n,连接BM,作MN⊥AB于N,
则∠CMB=∠CBM=45°,BM=$\sqrt{2}$n,
∴∠A+∠ABM=45°,
∵∠C=90°,AC=m,BC=n,
∴AB=$\sqrt{{m}^{2}+{n}^{2}}$,
∴$\frac{1}{2}$×AB×MN=$\frac{1}{2}$×AM×BC,即$\sqrt{{m}^{2}+{n}^{2}}$×MN=(m-n)×n,
解得,MN=$\frac{n(m-n)}{\sqrt{{m}^{2}+{n}^{2}}}$,
∴$\frac{BM}{MN}$=$\sqrt{2}$n×$\frac{\sqrt{{m}^{2}+{n}^{2}}}{n(m-n)}$=$\frac{\sqrt{2{m}^{2}+2{n}^{2}}}{m-n}$,
∵∠A+∠D=45°,∠A+∠ABM=45°,
∴∠D=∠ABM,又∠MNB=∠F=90°,
∴△EFD∽△MNB,
∴$\frac{DE}{EF}$=$\frac{BM}{MN}$=$\frac{\sqrt{2{m}^{2}+2{n}^{2}}}{m-n}$.
点评 本题考查的是相似三角形的判定和性质、勾股定理的应用,掌握相似三角形的判定定理和性质定理是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
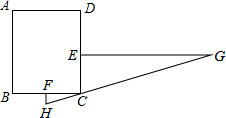 “今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形城池ABCD,城墙CD长 9 里,城墙BC长 7 里,东门所在的点E,南门所在的点F分别是CD,BC 的中点,EG⊥CD,EG=15里,FH⊥BC,点C在HG上,问FH等于多少里?答案是FH=1.05里.
“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形城池ABCD,城墙CD长 9 里,城墙BC长 7 里,东门所在的点E,南门所在的点F分别是CD,BC 的中点,EG⊥CD,EG=15里,FH⊥BC,点C在HG上,问FH等于多少里?答案是FH=1.05里.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com