
分析 将原方程整理成一般式得出a、b、c的值,计算判别式的值,再代入求根公式可得.
解答 解:(1)∵a=1,b=-2,c=-8,
∴△=4-4×1×(-8)=36>0,
则x=$\frac{2±6}{2}$,
∴x=4或x=-2;
(2)∵$\frac{3}{2}$y2+4y-1=0,
∴a=$\frac{3}{2}$,b=4,c=-1,
则△=16-4×$\frac{3}{2}$×(-1)=22>0,
∴x=$\frac{-4±\sqrt{22}}{3}$;
(3)∵3y2-2$\sqrt{3}$y+1=0,
∴a=3,b=-2$\sqrt{3}$,c=1,
则△=12-4×3×1=0,
∴x=$\frac{2\sqrt{3}}{6}$=$\frac{\sqrt{3}}{3}$;
(4)∵a=2,b=-5,c=1,
∴△=25-4×2×1=17>0,
则x=$\frac{5±\sqrt{17}}{4}$;
(5)∵a=-4,b=-8,c=1,
∴△=64-4×(-4)×1=80>0,
则x=$\frac{8±4\sqrt{5}}{-8}$=-$\frac{2±\sqrt{5}}{2}$;
(6)∵a=$\sqrt{2}$,b=-$\sqrt{3}$,c=-$\sqrt{2}$,
∴△=3-4×$\sqrt{2}$×(-$\sqrt{2}$)=11>0,
则x=$\frac{\sqrt{3}±\sqrt{11}}{2\sqrt{2}}$=$\frac{\sqrt{6}±\sqrt{22}}{4}$.
点评 本题主要考查公式法解一元二次方程,熟练掌握公式法解一元二次方程的步骤和求根公式是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | a>3 | B. | a≥3 | C. | a<3 | D. | a≤3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
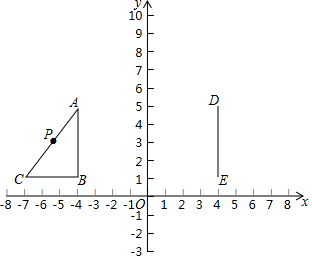 如图,在平面直角坐标系中,Rt△ABC的顶点A(-4,5),B(-4,1),∠B=90°,AC=5,点P是AC的中点,线段DE的两个端点坐标分别为D(4,5),E(4,1).
如图,在平面直角坐标系中,Rt△ABC的顶点A(-4,5),B(-4,1),∠B=90°,AC=5,点P是AC的中点,线段DE的两个端点坐标分别为D(4,5),E(4,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
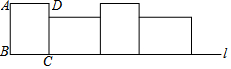 如图,矩形ABCD中,AB=4,BC=3,将矩形ABCD沿直线l右翻动(不滑动)至如图位置
如图,矩形ABCD中,AB=4,BC=3,将矩形ABCD沿直线l右翻动(不滑动)至如图位置查看答案和解析>>
科目:初中数学 来源: 题型:选择题
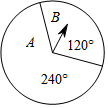 如图,让转盘自由转动一次,则指针落在A区域的概率是( )
如图,让转盘自由转动一次,则指针落在A区域的概率是( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2500(1+x)+2500(1+x)2=3600 | B. | 2500(1+x%)2=3600 | ||
| C. | 2500x2=3600 | D. | 2500(1+x)2=3600 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com