
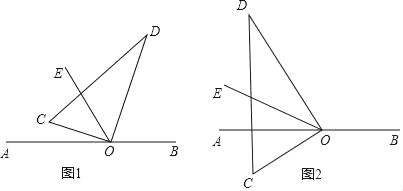
【题目】如图,直角三角板的直角顶点O在直线AB上,OC,OD是三角板的两条直角边,OE平分∠AOD.
(1)若∠COE=20°,则∠BOD= ;若∠COE=α,则∠BOD= (用含α的代数式表示)
(2)当三角板绕O逆时针旋转到图2的位置时,其它条件不变,试猜测∠COE与∠BOD之间有怎样的数量关系?并说明理由.
【答案】(1)40°;2α;(2)∠BOD=2∠COE.
【解析】试题分析:(1)先根据直角计算∠DOE的度数,再同角平分线的定义计算∠AOD的度数,最后利用平角的定义可得结论;
(2)设∠BOD=β,则∠AOD=180°-β,根据角平分线的定义表示∠BOE,再利用互余的关系求∠COE的度数,可得结论.
试题解析:(1)若∠COE=20°,
∵∠COD=90°,
∴∠EOD=90°﹣20°=70°,
∵OE平分∠AOD,
∴∠AOD=2∠EOD=140°,
∴∠BOD=180°﹣140°=40°;
若∠COE=α,
∴∠EOD=90﹣α,
∵OE平分∠AOD,
∴∠AOD=2∠EOD=2(90﹣α)=180﹣2α,
∴∠BOD=180°﹣(180﹣2α)=2α;
故答案为:40°;2α;
(2)如图2,∠BOD=2∠COE,理由是:
设∠BOD=β,则∠AOD=180°﹣β,
∵OE平分∠AOD,
∴∠EOD=![]() ∠AOD=
∠AOD=![]() =90°﹣
=90°﹣![]() ,
,
∵∠COD=90°,
∴∠COE=90°﹣(90°﹣![]() )=
)=![]() ,
,
即∠BOD=2∠COE.


科目:初中数学 来源: 题型:
【题目】线段EF是由线段PQ平移得到的,点P(-1,4)的对应点为E(4,7),则点Q(-3,1)的对应点F的坐标为( )
A. (-8,-2) B. (-2,2) C. (2,4) D. (-6,-1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区准备在每两幢楼房之间开辟绿地,其中有一块是面积为60m2的长方形绿地,并且长比宽多7m,求长方形的宽.若设长方形绿地的宽为xm,则可列方程为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=64°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为度. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MAN=120°,AC平分∠MAN.B,D分别在射线AN,AM上. 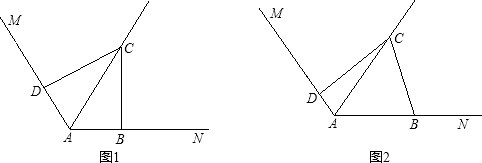
(1)在图(1)中,当∠ABC=∠ADC=90°时,求证:AD+AB=AC.
(2)若把(1)中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°,其他条件不变,如图(2)所示.则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB内任意一点,OP=5cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是5cm,则∠AOB的度数是( ) 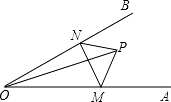
A.25°
B.30°
C.35°
D.40°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com