
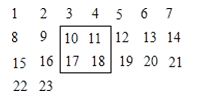
【题目】把2100个连续的正整数1、2、3、……、2100,按如图方式排列成一个数表,如图用一个正方形框在表中任意框住4个数,设左上角的数为x.
(1) 另外三个数用含x的式子表示出来,从小到大排列是___________
(2) 被框住4个数的和为416时,x值为多少?
(3) 能否框住四个数和为324?若能,求出x值;若不能,说明理由
(4) 从左到右,第1至第7列各数之和分别为a1、a2、a3、a4、a5、a6、a7,请直接写出7个数中最大的数与最小的数之差.
【答案】(1)x+1,x+7,x+8;(2)x=100;(3)不能;(4)1800.
【解析】试题分析:(1)根据数表的排列,可用含x的代数式表示出其它三个数;
(2)根据四个数之和为416,可得出关于x的一元一次方程,解之即可得出x的值,再由x不在第7列即可得出结论;
(3)根据四个数之和为324,可得出关于x的一元一次方程,解之即可得出x的值,再由x在第7列即可得出不存在用正方形框出的四个数的和为324;
(4)根据数表的排布,可得出总共300行其每行最右边的数比最左边的数大6,用其×300即可得出结论.
试题解析:解:(1)观察数表可知:另外三个数分别为x+1、x+7、x+8.
故答案为:x+1、x+7、x+8.
(2)设正方形框出的四个数中最小的数为x,根据题意得:x+(x+1)+(x+7)+(x+8)=416,解得:x=100.
∵100=14×7+2,∴100为第2列的数,符合题意.
答:被框住4个数的和为416时,x值为100.
(3)设正方形框出的四个数中最小的数为x,
根据题意得:x+(x+1)+(x+7)+(x+8)=324,解得:x=77,∴77=11×7,∴77为第7列的数,不符合题意,∴不存在用正方形框出的四个数的和为324.
(4)本数表共2100个数,每行7个数,共排300行,即有7列,每列共300个数,∵每一行最右边的数比最左边的数大6,∴a7﹣a1=6×(2100÷7)=1800.
答:7个数中最大的数与最小的数之差为1800.


科目:初中数学 来源: 题型:
【题目】现定义运算:对于任意有理数a、b,都有a![]() b=ab-b,如:2
b=ab-b,如:2![]() 3=2×3-3,请根据以上定义解答下列各题:
3=2×3-3,请根据以上定义解答下列各题:
(1) 2![]() (-3)=___________,x
(-3)=___________,x![]() (-2)=___________;
(-2)=___________;
(2) 化简:[(-x)![]() 3]
3] ![]() (-2);
(-2);
(3) 若x![]()
![]() =3
=3![]() (-x),求x的值.
(-x),求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
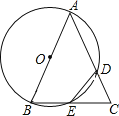
【题目】已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.
(1)求证:AB=AC;
(2)若AB=4,BC=![]() ,求CD的长.
,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用同样规格的黑白两色正方形瓷砖铺设矩形地面,请观察下列图形,探究并观察下列问题。
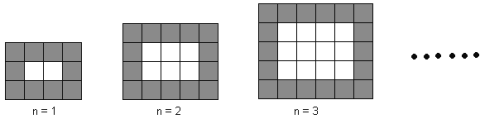
(1)在第4个图中,共有白色瓷砖 块;在第![]() 个图中,共有白色瓷砖 块;
个图中,共有白色瓷砖 块;
(2)在第4个图中,共有瓷砖 块;在第![]() 个图中,共有瓷砖 块;
个图中,共有瓷砖 块;
(3)如果每块黑瓷砖4元,白瓷砖3元,铺设当![]() 时,共需花多少钱购买瓷砖?
时,共需花多少钱购买瓷砖?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com