
【题目】如图,AB是⊙O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发沿着A→B→A方向运动,设运动时间为t(s)(0≤t<3),连接EF,当△BEF是直角三角形时,t(s)的值为【 】

A.![]() B.1 C.
B.1 C.![]() 或1 D.
或1 D.![]() 或1或
或1或![]()
【答案】D。
【解析】若△BEF是直角三角形,则有两种情况:①∠BFE=90°,②∠BEF=90°,分别讨论如下:
∵AB是⊙O的直径,∴∠ACB=90°。
Rt△ABC中,BC=2,∠ABC=60°,∴AB=2BC=4cm。
①当∠BFE=90°时;
Rt△BEF中,∠ABC=60°,则BE=2BF=2cm。
∴此时AE=AB-BE=2cm。
∵E点沿着A→B→A方向运动,∴E点运动的距离为:2cm或6cm。
∵点E以2cm/s的速度运动,∴t=1s或3s。
∵0≤t<3,∴t=3s不合题意,舍去。
∴当∠BFE=90°时,t=1s。
②当∠BEF=90°时,
同①可求得BE=![]() cm,此时AE=AB-BE=
cm,此时AE=AB-BE=![]() cm。
cm。
∵E点沿着A→B→A方向运动,∴E点运动的距离为:3.5cm或4.5cm。
∵点E以2cm/s的速度运动,∴t=![]() s或
s或![]() s(二者均在0≤t<3内)。
s(二者均在0≤t<3内)。
综上所述,当t的值为1、![]() 或
或![]() s时,△BEF是直角三角形。故选D。
s时,△BEF是直角三角形。故选D。


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】剪纸是中国传统的民间艺术,它画面精美,风格独特,深受大家喜爱,现有三张不透明的卡片,其中两张卡片的正面图案为“金鱼”,另外一张卡片的正面图案为“蝴蝶”,卡片除正面剪纸图案不同外,其余均相同.将这三张卡片背面向上洗匀从中随机抽取一张,记录图案后放回,重新洗匀后再从中随机抽取一张.请用画树状图(或列表)的方法,求抽出的两张卡片上的图案都是“金鱼”的概率.(图案为“金鱼”的两张卡片分别记为A1、A2,图案为“蝴蝶”的卡片记为B)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图1是一块边长为1,面积记为S1的正三角形纸板,沿图1的底边剪去一块边长为![]() 的正三角形纸板后得到图2,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的
的正三角形纸板后得到图2,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的![]() )后,得图3,图4,…,记第n(n≥3) 块纸板的面积为Sn,则S2018-S2019 =( )
)后,得图3,图4,…,记第n(n≥3) 块纸板的面积为Sn,则S2018-S2019 =( )
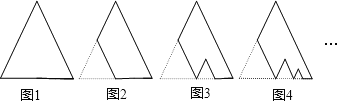
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
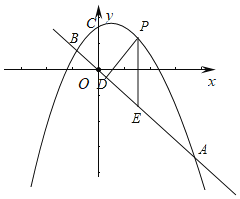
【题目】如图,已知抛物线y=-x2+bx+c与直线y=-x的交点A、B的横坐标分别为2和![]() .点P是直线上方抛物线上的一动点,过点P作PD⊥AB于点D,作PE⊥x轴交AB于点E.
.点P是直线上方抛物线上的一动点,过点P作PD⊥AB于点D,作PE⊥x轴交AB于点E.
(1)直接写出点A、B的坐标;
(2)求抛物线的关系式;
(3)判断△OBC形状,并说明理由;
(4)设点P的横坐标为n,线段PD的长为y,求y关于n的函数关系式;
(5)定义符号min{a,b)}的含义为:当a≥b时,min{a,b}=b;当a<b时,min{a,b}=a.如min{2,0}=0,min{-3,4}=-3.直接写出min{-x2+bx+c,-x}的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以AB为直径的⊙O交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,且DH是⊙O的切线,连接DE交AB于点F.
(1)求证:DC=DE;
(2)若AE=1,![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D是∠AOB的平分线OC上任意一点,过D作DE⊥OB于E,以DE为半径作⊙D,
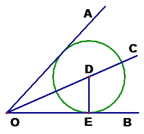
①判断⊙D与OA的位置关系, 并证明你的结论。
②通过上述证明,你还能得出哪些等量关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店用2500元采购A型商品的件数是用750元采购B种商品件数数量的2倍,已知一件A型商品的进价比一件B型商品的进价多10元.
(1)求一件A,B型商品的进价分别为多少元?
(2)若商店购进A,B型商品共150件,已知A型商品的售价为30元/件,B型商品的售价为25元/件,且全部售出,设购进A型商品m件,求这批商品的利润W(元)与m之间的函数关系式;
(3)在(2)的条件下,若A型商品的件数不少于B型商品的4倍,请你设计获利最大的进货方案,并求最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=x2+2x-3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,对称轴为直线l,点D(-4,n)在抛物线上.
(1)求直线CD的解析式;
(2)E为直线CD下方抛物线上的一点,连接EC,ED,当△ECD的面积最大时,在直线l上取一点M,过M作y轴的垂线,垂足为点N,连接EM,BN,若EM=BN时,求EM+MN+BN的值.
(3)将抛物线y=x2+2x-3沿x轴正方向平移得到新抛物线y′,y′经过原点O,y′与x轴的另一个交点为F,设P是抛物线y′上任意一点,点Q在直线l上,△PFQ能否成为以点P为直角顶点的等腰直角三角形?若能,直接写出点P的坐标,若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中踏集团销售某种商品,每件进价为10元。在销售过程中发现,平均每天的销售量y(件)与销售价x(元/件)(不低于进价)之间的关系可近似的看做一次函数:![]() ;
;
(1)求中踏集团平均每天销售这种商品的利润w(元)与销售价x之间的函数关系式;
(2)当这种商品的销售价为多少元时,可以获得最大利润,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com