练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

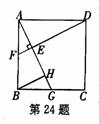
    如图，在正方形ABCD中，点G是边BC上的任意一点，DE⊥AG，垂足为E，延长DE交AB于点F．在线段AG上取点H，使得AG＝DE＋HG，连接BH．求证：∠ABH＝∠CDE．


    略

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如右图，下列不能判定∥的条件有(    ).

    A.∠3＝∠4              B.∠1＝∠5                                                                                                                                                                                                                

      C.∠1＋∠4＝180°       D.∠3＝∠5

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    图，在△ABC中，D是BC边上的一点，E是AD的中点，过点A作BC的平行线交CE的延长线于点F，且AF＝BD，连接BF．

      (1)线段BD与CD有何数量关系，为什么？

      (2)当△ABC满足什么条件时，四边形AFBD是矩形？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在Rt△ABC中，∠ACB＝90°，∠A＝α，将△ABC绕点C按顺时针方向旋转后得到△EDC，此时点D在AB边上，则旋转角的大小为_______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    解方程：

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算的结果是    (    )

      A．                  B．              C．              D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，□ABCD的对角线AC、BD相交于点O，试添加一个条件：______________，使得□ABCD为菱形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


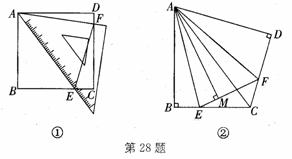
    如图①，等腰直角三角尺的一个锐角顶点与正方形ABCD的顶点A重合，将此三角尺绕点A旋转，使三角尺中该锐角的两条边分别交正方形的两边BC、DC于点E、F，连接EF．

        (1)猜想BE、EF、DF三条线段之间的数量关系，并证明你的猜想；

        (2)在图①中，过点A作AM⊥EF于点M，请直接写出AM和AB的数量关系；

    (3)如图②，将Rt△ABC沿斜边AC翻折得到Rt△ADC，E、F分别是BC、CD边上的点，∠EAF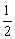＝∠BAD，连接EF，过点A作AM⊥EF于点M．试猜想AM与AB之间的数量关系，并证明你的猜想．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


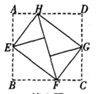
    如图，将矩形纸片ABCD的四个角向内翻折，恰好拼成一个无缝隙无重叠的四边形EFGH，若EH＝12厘米，EF＝16厘米，则边AD的长是    (    )

    A．12厘米            B．16厘米        C．20厘米        D．28厘米

    查看答案和解析>>

    同步练习册答案