
【题目】如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证: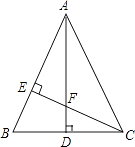
(1)△AEF≌△CEB;
(2)AF=2CD.
【答案】
(1)证明:∵AD⊥BC,CE⊥AB,
∴∠BCE+∠CFD=90°,∠BCE+∠B=90°,
∴∠CFD=∠B,
∵∠CFD=∠AFE,
∴∠AFE=∠B
在△AEF与△CEB中,
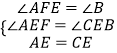 ,
,
∴△AEF≌△CEB(AAS)
(2)证明:∵AB=AC,AD⊥BC,
∴BC=2CD,
∵△AEF≌△CEB,
∴AF=BC,
∴AF=2CD
【解析】(1)根据垂直的定义得出∠BCE+∠CFD=90°,∠BCE+∠B=90°,根据同角的余角相等得出∠CFD=∠B,然后由AAS判断出△AEF≌△CEB;
(2)等腰三角形的三线合一得出BC=2CD,根据全等三角形的性质得出AF=BC,从而得出AF=2CD。
【考点精析】关于本题考查的余角和补角的特征和垂线的性质,需要了解互余、互补是指两个角的数量关系,与两个角的位置无关;垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】下列分解因式正确的是( )
A.﹣a+a3=﹣a(1+a2)
B.2a﹣4b+2=2(a﹣2b)
C.a2﹣4=(a﹣2)2
D.a2﹣2a+1=(a﹣1)2
查看答案和解析>>
科目:初中数学 来源: 题型:
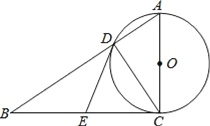
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O,与斜边AB交于点D、E为BC边的中点,连接DE.
(1)求证:DE是⊙O的切线;
(2)填空:①若∠B=30°,AC=2![]() ,则DE= ;
,则DE= ;
②当∠B= °时,以O,D,E,C为顶点的四边形是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】浙江卫视《中国好声音》总决赛,全国有7100人通过电视收看,这个数据用科学记数法表示为( )
A.71×102
B.7.1×102
C.7.1×103
D.0.71×104
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,点P(-2,3)关于x轴对称的点的坐标为( )
A. (3,-2) B. (2,-3) C. (-3,2) D. (-2,-3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种肥皂售价为每块2元,凡购买两块以上(含两块),商场推出两种优惠销售方法.第一种:“1块按原价,其余按原价的七折优惠”;第二种:“全部按原价的八折优惠”.你在购买相同数量的肥皂的情况下,要使第一种方法比第二种方法得到的优惠多,最少要购买肥皂( )块 .
A. 4B. 5C. 6D. 7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com