
分析 根据有理数的混合运算法则计算即可.
解答 解:(1)3$\frac{1}{2}$-(-2$\frac{1}{4}$)+(-$\frac{1}{3}$)-$\frac{1}{4}$-(+$\frac{1}{6}$)
=3$\frac{1}{2}$+2$\frac{1}{4}$-$\frac{1}{3}$-$\frac{1}{4}$-$\frac{1}{6}$
=3$\frac{1}{2}$+2-$\frac{1}{2}$
=5;
(2)(+17$\frac{3}{4}$)+(-9$\frac{5}{11}$)-(+2.25)-(+17.7)+(-10$\frac{6}{11}$)
=(-9$\frac{5}{11}$-10$\frac{6}{11}$)+(17.75-2.25)-17.7
=-20+15.5-17.7
=-20-2.2
=-22.2;
(3)($\frac{1}{4}$-$\frac{1}{2}$-$\frac{1}{6}$)×(-12)
=-$\frac{1}{4}$×12+$\frac{1}{2}×$12+$\frac{1}{6}$×12
=-3+6+2
=5;
(4)13-[26-(-21)+(-18)]
=13-(26+21-18)
=13-29
=-16;
(5)[1.4-(-3.6+5.2)-4.3]-(-1.5)
=1.4-1.6-4.3+1.5
=2.9-5.9
=-3;
(6)|-7$\frac{3}{8}$+4$\frac{1}{3}$|+18$\frac{1}{4}$+|-6-$\frac{1}{3}$|
=7$\frac{3}{8}$-4$\frac{1}{3}$+18$\frac{1}{4}$+6+$\frac{1}{3}$
=(7$\frac{3}{8}$+18$\frac{1}{4}$)-(4$\frac{1}{3}$$-\frac{1}{3}$)+6
=15$\frac{5}{8}$-4+6
=17$\frac{5}{8}$.
点评 本题考查的是有理数的混合运算,掌握有理数的混合运算法则是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
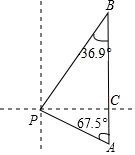 马航MH370 客机“失联”,我国“海巡01号”前往搜寻.如图某天上午9时,“海巡01号”轮船位于A处,观测到某小岛P位于轮船的北偏西67.5°,轮船以21海里/时的速度向正北方向行驶,下午2时该船到达B处,这时观测到小岛P位于该船的南偏西36.9°方向,求轮船行驶过程中与小岛P的最短距离PC.
马航MH370 客机“失联”,我国“海巡01号”前往搜寻.如图某天上午9时,“海巡01号”轮船位于A处,观测到某小岛P位于轮船的北偏西67.5°,轮船以21海里/时的速度向正北方向行驶,下午2时该船到达B处,这时观测到小岛P位于该船的南偏西36.9°方向,求轮船行驶过程中与小岛P的最短距离PC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com