
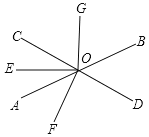
【题目】如图,直线AB与CD相交于O,OE是∠AOC的平分线,OF⊥CD,OG⊥OE,∠BOD=52°.
(1)求∠AOC,∠AOF的度数;
(2)求∠EOF与∠BOG是否相等?请说明理由.
【答案】(1)∠AOC=52°,∠AOF=38°;(2)相等,理由见解析.
【解析】
(1)直接利用垂直的定义结合对顶角的定义得出∠AOC,∠AOF的度数;
(2)分别求出∠EOF与∠BOG的度数进而得出答案.
(1)∵OF⊥CD,
∴∠COF=90°,
又∵∠AOC与∠BOD是对顶角,
∴∠AOC=∠BOD=52°,
∴∠AOF=∠COF-∠AOC=90°-52°=38°;
(2)相等,
理由:∵∠AOC与∠BOD是对顶角,
∴∠AOC=∠BOD=52°,
∵OE是∠AOC的平分线,
∴∠AOE=![]() ∠AOC=26°,
∠AOC=26°,
又∵OG⊥OE,
∴∠EOG=90°,
∴∠BOG=180°-∠AOE-∠EOG=64°,
∵∠EOF=∠AOF+∠AOE=38°+26°=64°,
∴∠EOF=∠BOG.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】一个电子跳蚤从数轴的原点出发,连续不断地一左一右来回跳动(第一次向左跳),跳动的距离依次为![]() ,
,![]() ,
,![]() ,
,![]() …
…
(1)如果![]() 是正整数,那么第
是正整数,那么第![]() 次跳动的距离是______;
次跳动的距离是______;
(2)第![]() 次跳动的落点位置所对应的有理数是______;
次跳动的落点位置所对应的有理数是______;
(3)第![]() 次跳动后所处位置在原点的______侧;
次跳动后所处位置在原点的______侧;
(4)①相对于出发点,电子跳蚤第一次跳记作![]() (向左跳),第二次跳记作
(向左跳),第二次跳记作![]() (向右跳),以此类推,如果
(向右跳),以此类推,如果![]() 是正整数,那么第
是正整数,那么第![]() 次记作______;
次记作______;
②会不会有相邻两次跳动的落点位置在原点的同侧?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,点A(1,1),B(3,1),C(3,2),反比例函数y=![]() (x>0)的图象经过点D,且与AB相交于点E,
(x>0)的图象经过点D,且与AB相交于点E,

(1)求反比例函数的解析式;
(2)过点C、E作直线,求直线CE的解析式;
(3)如图2,将矩形ABCD沿直线CE平移,使得点C与点E重合,求线段BD扫过的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)当∠BQD=30°时,求AP的长;
(2)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.

(1)试说明DF是⊙O的切线;
(2)若AC=3AE,求tanC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点O为直线AB上一点,将直角三角板MON的直角顶点放在点O处,并在∠MON内部作射线OC.
(1)将三角板放置到如图所示位置,使OC恰好平分∠MOB,且∠BON=2∠NOC,求∠AOM的度数;
(2)若仍将三角板按照如图所示的方式放置,仅满足OC平分∠MOB,试猜想∠AOM与∠NOC之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC为等腰直角三角形,∠ACB=90,F是AC边上的一个动点(点F与A. C不重合),以CF为一边在等腰直角三角形外作正方形CDEF,连接BF、AD.
(1)猜想图1中线段BF、AD的数量关系及所在直线的位置关系,直接写出结论;
(2)将图1中的正方形CDEF,绕着点C按顺时针方向旋转任意角度α,得到如图2的情形。图2中BF交AC于点H,交AD于点O,请你判断(1)中得到的结论是否仍然成立,并证明你的判断。
(3)将原题中的等腰直角三角形ABC改为直角三角形ABC,∠ACB=90,正方形CDEF改为矩形CDEF,如图3,且AC=4,BC=3,CD=![]() ,CF=1,BF交AC于点H,交AD于点O,连接BD、AF,求BD2+AF2的值。
,CF=1,BF交AC于点H,交AD于点O,连接BD、AF,求BD2+AF2的值。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小娟玩游戏:一张纸片,第一次将其撕成四个正方形片,手中共有4张纸片,以后每次都将其中一片撕成更小的四个正方形片.如此进行下去,根据上述情况:

(1)当撕10次时,小娟手中共有 张纸;
(2)当小娟撕到第n次时,手中共有S张纸片,请用含n的代数式表示S;
(3)小娟手中能否有2020张纸片?如果能,请算出是第几次撕;如果不能,需说明理由.
(4)如果设原正方形的边长为1,通过不断地分割该面积为1的正方形,并把数量关系和几何图形巧妙地结合起来,可以很容易得到一些计算结果,请结合上图计算![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com