

|
|
|
|


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:广东省中考真题 题型:解答题

查看答案和解析>>
科目:初中数学 来源:同步题 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:
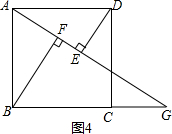
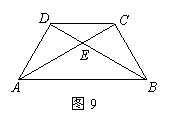
将两块大小一样含30°角的直角三角板,叠放在一起,使得它们的斜边
AB重合,直角边不重合,已知AB=8,BC=AD=4,AC与BD相交于点E,连结CD.
(1)填空:如图9,AC= ,BD= ;四边形ABCD是 梯形.
(2)请写出图9中所有的相似三角形(不含全等三角形).
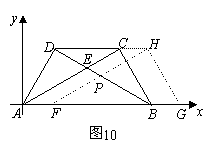
(3)如图10,若以AB所在直线为![]() 轴,过点A垂直于AB的直线为
轴,过点A垂直于AB的直线为![]() 轴建立如图10的平面直角坐标系,保持ΔABD不动,将ΔABC向
轴建立如图10的平面直角坐标系,保持ΔABD不动,将ΔABC向![]() 轴的正方向平移到ΔFGH的位置,FH与BD相交于点P,设AF=t,ΔFBP面积为S,求S与t之间的函数关系式,并写出t的取值值范围.
轴的正方向平移到ΔFGH的位置,FH与BD相交于点P,设AF=t,ΔFBP面积为S,求S与t之间的函数关系式,并写出t的取值值范围.
 | |||
 | |||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com