

分析 (1)延长NC到E,使CE=BM,连接DE,先证△CDE≌△BDM,再证△DMN≌△DEN;
(2)在CA上截取CE=BM,连接DE,先证△MBD≌△ECD,再证△NMD≌△NED;
解答 解:(1)MN=BM+CN.
如图1,延长NC到E,使CE=BM,连接DE,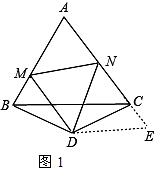
∵△ABC为等边三角形,△BCD为等腰三角形,且∠BDC=120°,
∴∠MBD=∠MBC+∠DBC=60°+30°=90°,
∴∠DCE=180°-∠ACD=180°-∠ABD=90°,
在△CDE和△BDM中,
$\left\{\begin{array}{l}{CD=BD}\\{∠MBD=∠ECD}\\{CE=BM}\end{array}\right.$,
∴△CDE≌△BDM(SAS),
∴∠CDE=∠BDM,DE=DM,
∴∠NDE=∠NDC+∠CDE=∠NDC+∠BDM=∠BDC-∠MDN=120°-60°=60°,
在△DMN和△DEN中,
$\left\{\begin{array}{l}{DM=DE}\\{∠MDN=∠EDN}\\{DN=DN}\end{array}\right.$,
∴△DMN≌△DEN(SAS),
∴MN=NE=CE+CN=BM+CN.
(2)MN=CN-BM.
如图2,在CA上截取CE=BM,连接DE,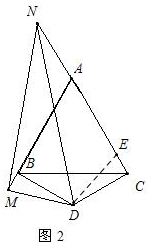
在△MBD和△ECD中,
$\left\{\begin{array}{l}{MB=EC}\\{∠MBD=∠ECD}\\{BD=CD}\end{array}\right.$,
∴△MBD≌△ECD(SAS),
∴DM=DE,∠MDB=∠EDC,
∵∠MDN=∠MDB+∠BDN=∠CDE+∠BDN=60°,
∴∠EDN=60°=∠MDN,
在△NMD和△NED中,
$\left\{\begin{array}{l}{MD=ED}\\{∠MDN=∠EDN}\\{ND=ND}\end{array}\right.$,
∴△NMD≌△NED(SAS),
∴NE=MN,
∴MN=CN-CE=CN-BM.
点评 本题主要考查了等边三角形和等腰三角形的性质、全等三角形的判定与性质,难度适中.对于线段和差等式的证明,截长补短是关键.


科目:初中数学 来源: 题型:选择题
 一个几何体由几个大小相同的小立方块搭成,从左面和从上面看到的这个几何体的形状如图所示,那么构成这个几何体的小立方块最多有( )个.
一个几何体由几个大小相同的小立方块搭成,从左面和从上面看到的这个几何体的形状如图所示,那么构成这个几何体的小立方块最多有( )个.| A. | 4个 | B. | 5个 | C. | 6个 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小玲用下面的方法来测量学校教学大楼AB的高度:如图,在水平地面上放一面平面镜,镜子与教学大楼的距离EA=25米.当她与镜子的距离CE=2.5米时,她刚好能从镜子中看到教学大楼的顶端B.已知她的眼睛距地面高度DC=1.6米.请你帮助小玲计算出教学大楼的高度AB是多少米(注意:根据光的反射定律:反射角等于入射角).
小玲用下面的方法来测量学校教学大楼AB的高度:如图,在水平地面上放一面平面镜,镜子与教学大楼的距离EA=25米.当她与镜子的距离CE=2.5米时,她刚好能从镜子中看到教学大楼的顶端B.已知她的眼睛距地面高度DC=1.6米.请你帮助小玲计算出教学大楼的高度AB是多少米(注意:根据光的反射定律:反射角等于入射角).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com