
【题目】计算与解方程
(1)|﹣3|+( ![]() ﹣1)0﹣
﹣1)0﹣ ![]() +(
+( ![]() )﹣1;
)﹣1;
(2)解方程组 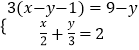 ;
;
(3)求x的值:25(x+2)2﹣36=0.
【答案】
(1)解:原式=3+1﹣4+3
=3
(2)解:原方程可化为 ![]()
①+②得6x=24,
解得x=,4
把x=4代入①得y=0,
所以,原方程组的解为 ![]()
(3)解:方程整理得:(x+2)2= ![]() ,
,
开方得:x+2=± ![]() ,
,
解得:x1=﹣ ![]() ,x2=﹣
,x2=﹣ ![]()
【解析】(1)原式利用立方根的绝对值的性质,零指数幂、负指数幂以及平方根定义化简,然后即可计算出结果.(2)原方程组变形后,直接利用加减消元法从而求出x的值,然后把x的值代入一方程求y的值;(3)方程整理后,利用平方根定义开方即可求出解.
【考点精析】解答此题的关键在于理解零指数幂法则的相关知识,掌握零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数),以及对整数指数幂的运算性质的理解,了解aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数).


科目:初中数学 来源: 题型:
【题目】如图1,△ABC是等腰直角三角形,∠BAC= 90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.

(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长DB交CF于点H.
①求证:BD⊥CF;
②当AB=2,AD=3![]() 时,求线段DH的长.
时,求线段DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知多项式(17x2﹣3x+4)﹣(ax2+bx+c)能被5x整除,且商式为2x+1,则a﹣b+c=( )
A. 12 B. 13 C. 14 D. 19
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种牛奶包装盒标明“净重300g,蛋白质含量≥2.9%”.那么其蛋白质含量为()
A. 2.9%及以上 B. 8.7g C. 8.7g及以上 D. 不足8.7g
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校组织同学们春游,租用45座和30座两种型号的客车,若租用45座客车x辆,租用30座客车y辆,则不等式“45x+30y≥500”表示的实际意义是( )
A. 两种客车总的载客量不少于500人 B. 两种客车总的载客量不超过500人
C. 两种客车总的载客量不足500人 D. 两种客车总的载客量恰好等于500人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年我市某公司分两次采购了一批大蒜,第一次花费40万元,第二次花费60万元.已知第一次采购时每吨大蒜的价格比去年的平均价格上涨了500元,第二次采购时每吨大蒜的价格比去年的平均价格下降了500元,第二次的采购数量是第一次采购数量的两倍.
(1)试问去年每吨大蒜的平均价格是多少元?
(2)该公司可将大蒜加工成蒜粉或蒜片,若单独加工成蒜粉,每天可加工8吨大蒜,每吨大蒜获利1000元;若单独加工成蒜片,每天可加工12吨大蒜,每吨大蒜获利600元.由于出口需要,所有采购的大蒜必需在30天内加工完毕,且加工蒜粉的大蒜数量不少于加工蒜片的大蒜数量的一半,为获得最大利润,应将多少吨大蒜加工成蒜粉?最大利润为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com