
����Ŀ��ijѧУ����չ����������������������������������Ŀ������ƹ�����������ë��Ҫ��ÿλѧ��������ֻ��ѡ��һ�Ϊ�˽�ѡ������������Ŀ��ѧ�������������ȡ�˲���ѧ�����е��飬����ͨ�������õ����ݽ������������Ƴ�����������������ͳ��ͼ�������ͳ��ͼ�ش����⣺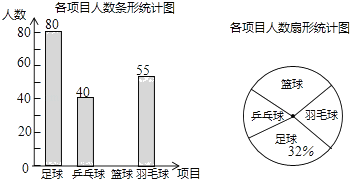
��1����λһ����������ѧ����
��2����ȫ����ͳ��ͼ��
��3��������ͳ��ͼ�У�ѡ��������Ŀ�������������ε�Բ�Ľǵ����ȣ�
��4������ѧУ��1500�ˣ�������Ƹ�ѧУѡ��������Ŀ��ѧ������Լ���ˣ�
���𰸡�
��1��250
��2��
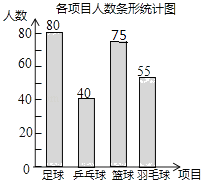
��3��108
��4��480
���������⣺��1����λһ������ѧ����80��32%=250���ˣ�����2��ѡ����������Ϊ��250��80��40��55=75���ˣ���
��ȫ����ͼ��ͼ�� ����3��ѡ��������Ŀ�������������ε�Բ�Ľ�Ϊ��
����3��ѡ��������Ŀ�������������ε�Բ�Ľ�Ϊ�� ![]() ��360��=108�㣻��4�����Ƹ�ѧУѡ��������Ŀ��ѧ������Լ�ǣ�1500��32%=480���ˣ���
��360��=108�㣻��4�����Ƹ�ѧУѡ��������Ŀ��ѧ������Լ�ǣ�1500��32%=480���ˣ���
�ʴ�Ϊ����1��250����3��108����4��480��
��1���ɡ�������������ٷֱȿɵ�����������2�����ݸ���Ŀ����֮�͵��������������������������ȫͼ�μ��ɣ���3���á���������ռ�����������ı�������360�㼴�ɣ���4��������������������������ռ�ٷֱȼ��ɵã�


 �����ҵ���������ϵ�д�
�����ҵ���������ϵ�д� �����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�
�����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д� �����ҵ�����������ѧ���ӳ�����ϵ�д�
�����ҵ�����������ѧ���ӳ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
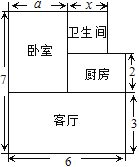
����Ŀ������������ɳƺ�ӹ���һ��С������Ʒ������ȥij¥���˽������֪���û�����Ʒ���ĵ�����12000Ԫ/m2�������ͼ��ʾ����λ���ף����ҵĿ�Ϊa�ף�������Ŀ�Ϊx�ף���
(1) �ú�a��x��ʽ�ӱ�ʾ�û��͵����
(2) �۷���Ϊ�������ṩ�����������Żݷ�����
����һ�������ĵ�����12 000Ԫ/m2�����г���ֻ��![]() �����;
�����;
��������������ԭ�����ܽ���9�۳���,
������������Ļ���a��3���ҷֱ������ַ������������ȣ���x��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC �У�AB=AC����C=70�㣬��AB��C������ABC ����ֱ�� EF�Գƣ���CAF=10�㣬���� BB�������ABB���Ķ����ǣ� ��
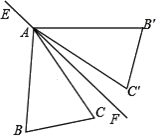
A. 30�� B. 35�� C. 40�� D. 45��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ABC=90�㣬AB=8��BC=6����DE�ǡ�ABC����λ�ߣ��ӳ�DE����ABC����ǡ�ACM��ƽ�����ڵ�F�����߶�DF�ij�Ϊ�� ��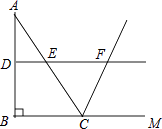
A.7
B.8
C.9
D.10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
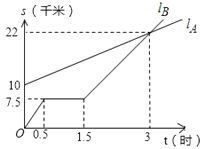
����Ŀ����ͼ��lA��lB�ֱ��ʾA������B�ﳵ��ͬһ·����ʻ��·��S��ʱ��t�Ĺ�ϵ��
��1��B����ʱ��A���______ǧ�ף�
��2��B����һ��·�����г��������ϣ��������������õ�ʱ����______Сʱ��
��3��B������______Сʱ��A������
��4����B�����г����������ϣ����ֳ���ʱ���ٶ�ǰ����______Сʱ��A��������������B�ij�����______ǧ�ף���ͼ�б�ʾ�����������C��
��5�����A���ߵ�·��S��ʱ��t�ĺ�����ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ǿ��Խ�������λ����ʾΪ![]() ������a��b��c �ֱ��ʾ��λ�ϵ����֣�ʮλ�ϵ����ֺ�λ�ϵ����֣���a
������a��b��c �ֱ��ʾ��λ�ϵ����֣�ʮλ�ϵ����ֺ�λ�ϵ����֣���a![]() 0����Ȼ��
0����Ȼ��![]() = 100a+10b+c�����ǰ�����
= 100a+10b+c�����ǰ�����![]() ��
��![]() ��������λ����Ϊһ�����������������x��y��z��������������Ȼ�����磺123��321��һ�����������,789��987��һ�����������.
��������λ����Ϊһ�����������������x��y��z��������������Ȼ�����磺123��321��һ�����������,789��987��һ�����������.
��1��һ������������ĺ�Ϊ1110����������������.
��2�������x��ʾ��λ���֣���˵��������һ������������ĺ��ܱ�37����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��I�ǡ�ABC�����ģ�AI���ӳ��ߺ͡�ABC�����Բ�ཻ�ڵ�D������BI��BD��DC������˵���д����һ���ǣ������� 
A.�߶�DB�Ƶ�D˳ʱ����תһ�������߶�DC�غ�
B.�߶�DB�Ƶ�D˳ʱ����תһ�������߶�DI�غ�
C.��CAD�Ƶ�A˳ʱ����תһ�������DAB�غ�
D.�߶�ID�Ƶ�I˳ʱ����תһ�������߶�IB�غ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
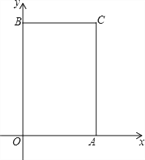
����Ŀ����֪��A��a��0����B��0��b������![]() ���ֱ����A��B��x�ᡢy��Ĵ��߽��ڵ�C����ͼ����P��ԭ���������ÿ��2����λ���ȵ��ٶ�����O-B-C-A-O��·���ƶ���
���ֱ����A��B��x�ᡢy��Ĵ��߽��ڵ�C����ͼ����P��ԭ���������ÿ��2����λ���ȵ��ٶ�����O-B-C-A-O��·���ƶ���
��1��д��A��B��C��������ꣻ
��2������P�ƶ���6��ʱ�������ʱP���λ�ã���д����P��λ�����ꣻ
��3�����ᣨ2����B��P���㣬���߶�BP����ƽ��h����λ��h��0�����õ�B��P�䣬��B��P�佫�ı���OACB���ܳ��ֳ���ȵ������֣���h��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��O��ֱ����BF�С�O�ڵ�B��AF����O�ڵ�D����C��DF�ϣ�BC����O�ڵ�E���ҡ�BAF=2��CBF��CG��BF�ڵ�G������AE�� 
��1��ֱ��д��AE��BC��λ�ù�ϵ��
��2����֤����BCG�ס�ACE��
��3������F=60�㣬GF=1�����O�İ뾶����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com