
分析 利用二次函数的性质得到抛物线的对称轴为直线x=3,则根据抛物线的对称性得到抛物线与x轴的两交点坐标为(2,0),(4,0),于是可设交点式y=a(x-2)(x-4),然后把顶点坐标代入求出a的值即可.
解答 解:根据题意得抛物线的对称轴为直线x=3,
而抛物线与x轴两交点之间的距离为2,
所以抛物线与x轴的两交点坐标为(2,0),(4,0),
设抛物线解析式为y=a(x-2)(x-4),
把(3,1)代入得a•1•(-1)=1,解得a=-1,
所以抛物线的解析式为y=-(x-2)(x-4),即y=-x2+6x-8.
点评 本题考查了用待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解,


科目:初中数学 来源: 题型:解答题
 已知抛物线y1=-(x+1)2+4.
已知抛物线y1=-(x+1)2+4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
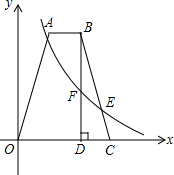 如图,在四边形OABC中,AB∥OC,OA=BC,点B,C的坐标分别为(4,8),(6,0),E为BC上一点,且BE=3CE,过点B作BD⊥x轴于点D.双曲线y=$\frac{k}{x}$(x>0)经过点E,且交BD于点F.
如图,在四边形OABC中,AB∥OC,OA=BC,点B,C的坐标分别为(4,8),(6,0),E为BC上一点,且BE=3CE,过点B作BD⊥x轴于点D.双曲线y=$\frac{k}{x}$(x>0)经过点E,且交BD于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
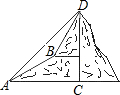 如图,甲乙两数学兴趣小组测量出CD的高度,甲小组在地面A处测量,乙小组在上坡B处测量,AB=200m,甲小组测得山顶D的仰角为45°,山坡B处的仰角为30°;乙小组测得山顶D的仰角为58°,求山CD的高度(结果保留一位小数)
如图,甲乙两数学兴趣小组测量出CD的高度,甲小组在地面A处测量,乙小组在上坡B处测量,AB=200m,甲小组测得山顶D的仰角为45°,山坡B处的仰角为30°;乙小组测得山顶D的仰角为58°,求山CD的高度(结果保留一位小数)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
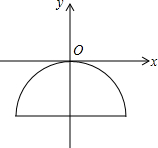 如图,一抛物线型石拱桥在如图所示的直角坐标系中,桥的最大高度是16米,跨度是46米.
如图,一抛物线型石拱桥在如图所示的直角坐标系中,桥的最大高度是16米,跨度是46米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com