
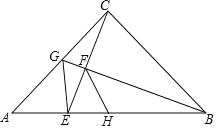
【题目】如图,△ABC中,∠ACB=90°,AC=BC,点G为AC中点,连结BG,CE⊥BG于F,交AB于E,连接GE,点H为AB中点,连接FH.以下结论:(1)∠ACE=∠ABG;(2)∠AGE=∠CGB:(3)若AB=10![]() ,则BF=4
,则BF=4![]() ;(4)FH平分∠BFE;(5)S△BGC=3S△CGE.其中正确结论的个数是( )
;(4)FH平分∠BFE;(5)S△BGC=3S△CGE.其中正确结论的个数是( )
A.1B.2C.3D.4
【答案】D
【解析】
如图,作AP⊥AC交CE的延长线于P,连接CH.构造全等三角形,证明△CAP≌△BCG(ASA),△EAG≌△EAP(SAS),即可判断(2)(5)正确,利用相似三角形的判定与性质可以证明(4)正确,解直角三角形可以判定(3)正确.
如图,作AP⊥AC交CE的延长线于P,连接CH.

∵CE⊥BG,
∴∠CFB=∠ACB=90°.
∵∠ACE+∠BCE=90°,∠CBG+∠BCE=90°,
∴∠ACE=∠CBG.
∵BG是△ABC的中线,AB>BC,
∴BG不是∠ACB的角平分线,
∴∠ABG≠∠CBG,
∴∠ACE≠∠ABG,故(1)错误.
∵∠ACP=∠CBG,AC=BC,∠CAP=∠BCG=90°,
∴△CAP≌△BCG(ASA),
∴CG=PA=AG,∠BGC=∠P.
∵AG=AP,∠EAG=∠EAP=45°,AE=AE,
∴△EAG≌△EAP(SAS),
∴∠AGE=∠P,
∴∠AGE=∠CGB,故(2)正确.
∵AB=10![]() ,△ABC是等腰直角三角形,
,△ABC是等腰直角三角形,
∴AC=BC=10,
∴AG=CG=5,
∴BG![]()
![]() CGCB
CGCB![]() CF,
CF,
∴CF=2![]() ,
,
∴BF![]() ,故(3)正确.
,故(3)正确.
∵CA=CB,∠ACB=90°,AH=HB,
∴∠BCH=∠ACH=45°.
∵∠CFB=∠CHB=90°,∠COF=∠BOH,
∴△COF∽△BOH,
∴CO:OF=BO:OH.
∵∠COB=∠FOH,
∴△COB∽△FOH,
∴∠HFB=∠BCH=45°,
∴∠EFH=∠HFB=45°,
∴FH平分∠BFE,故(4)正确.
∵AG=GC,
∴S△CGE=S△AEG.
∵△AEG≌△AEP,
∴S△AEG=S△AEP,
∴S△GCE![]() S△ACP.
S△ACP.
∵△CAP≌△CBG,
∴S△ACP=S△CBG,
∴S△BGC=3S△CGE.故(5)正确.
故选D.


科目:初中数学 来源: 题型:
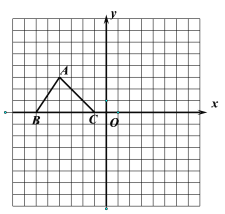
【题目】如图,已知△ABC的三个顶点坐标为A(-4,3)、B(-6,0)、C(-1,0).
(1) 请画出△ABC关于坐标原点O的中心对称图形△A′B′C′,并写出点A的对应点A′的坐标 ;
(2)若将点B绕坐标原点O顺时针旋转90°,请直接写出点B的对应点B″的坐标 ;
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
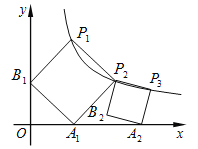
【题目】如图,正方形![]() 的顶点
的顶点![]() 、
、![]() 在反比例函数
在反比例函数![]() 的图象上,顶点
的图象上,顶点![]() 、
、![]() 分别在
分别在![]() 轴、
轴、![]() 轴的正半轴上,再在其右侧作正方形
轴的正半轴上,再在其右侧作正方形![]() ,顶点
,顶点![]() 在反比例函数
在反比例函数![]() 的图象上,顶点
的图象上,顶点![]() 在
在![]() 轴的正半轴上,则点
轴的正半轴上,则点![]() 的坐标为____.
的坐标为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.
(1)求证:△ABC≌△ADE;
(2)求∠FAE的度数;
(3)求证:CD=2BF+DE.

查看答案和解析>>
科目:初中数学 来源: 题型:
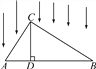
【题目】如图所示,△ABC被平行光线照射,CD⊥AB于D,AB在投影面上.
(1)指出图中AC的投影是什么?CD与BC的投影呢?
(2)探究:当△ABC为直角三角形(∠ACB=90°)时,易得AC2=AD·AB,此时有如下结论:直角三角形一直角边的平方等于它在斜边射影与斜边的乘积,这一结论我们称为射影定理.通过上述结论的推理,请证明以下两个结论.
①BC2=BD·AB;②CD2=AD·BD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,同时将点A(﹣1,0)、B(3,0)向上平移2个单位长度再向右平移1个单位长度,分别得到A、B的对应点C、D.连接AC,BD

(1)求点C、D的坐标,并描出A、B、C、D点,求四边形ABDC面积;
(2)在坐标轴上是否存在点P,连接PA、PC使S△PAC=S四边形ABCD?若存在,求点P坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
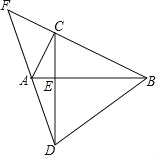
【题目】如图,Rt△ABC中,∠ACB=90°,CD⊥AB于E,CD=AB,DA、BC延长线交于F.
(1)若AC=12,∠ABC=30°,求DE的长;
(2)若BC=2AC,求证:DA=![]() FC.
FC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,三角形![]() (记作
(记作![]() )在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是
)在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是![]() ,
,![]() ,
,![]() ,先将
,先将![]() 向上平移3个单位长度,再向右平移2个单位长度,得到
向上平移3个单位长度,再向右平移2个单位长度,得到![]() .
.

(1)在图中画出![]() ;
;
(2)点![]() ,
,![]() 的坐标分别为______、______;
的坐标分别为______、______;
(3)若![]() 轴有一点
轴有一点![]() ,使
,使![]() 与
与![]() 面积相等,求出
面积相等,求出![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
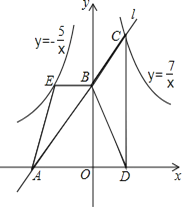
【题目】如图,在平面直角坐标系xOy中,直线l交x轴和y轴于点A,B,反比例函数y=![]() (x>0)的图象于点C,过点C作y轴的平行线交x轴于点D,过点B作x轴的平行线交反比例函数y=-
(x>0)的图象于点C,过点C作y轴的平行线交x轴于点D,过点B作x轴的平行线交反比例函数y=-![]() (x<0)的图象于点E,则图中阴影部分的总面积为______.
(x<0)的图象于点E,则图中阴影部分的总面积为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com