
某中学开展“绿化家乡、植树造林”活动,为了解全校植树情况,对该校甲、乙、丙、丁四个班级植树的棵树和所占百分比情况进行了调查,将收集的数据整理并绘制成图1和图2两幅不完整的统计图,请根据图中的信息,完成下列问题:
(1)这四个班共植树 棵;
(2)请补全两幅统计图;
(3)若四个班级植树的平均成活率是95%,全校共植树2000棵,请你估计全校种植的树中成活的树大约有多少棵?
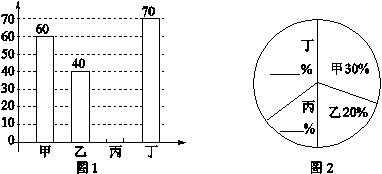
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:初中数学 来源: 题型:
概念:点P、Q分别是两条线段a和b上任意一点,线段PQ长度的最小值叫做线段a与线段b的
“理想距离”.已知O(0,0),A(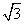 ,1),B(m,n),C(m,n+2)是平面直角坐标系中四点.
,1),B(m,n),C(m,n+2)是平面直角坐标系中四点.
(1) 根据上述概念,根据上述概念,完成下面的问题(直接写答案)
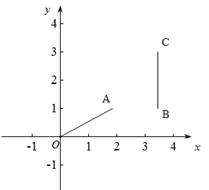
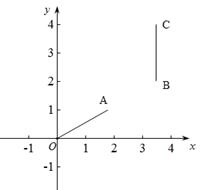
① 当m=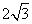 ,n=1时,如图13-1,线段BC与线段OA的理想距离是 2
,n=1时,如图13-1,线段BC与线段OA的理想距离是 2
;
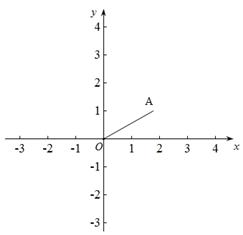
② 当m=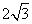 ,n=2时,如图13-2,线段BC与线段OA的理想距离为 ;
,n=2时,如图13-2,线段BC与线段OA的理想距离为 ;
③ 当m=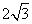 ,若线段BC与线段OA的理想距离为
,若线段BC与线段OA的理想距离为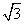 ,则n的取值范围是 .
,则n的取值范围是 .
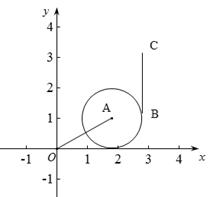
(2)如图13-3,若点B落在圆心为A,半径为1的圆上,
当n≥1时,线段BC与线段OA的理想距离记为d,则d的最小值为 (说明理由)
 (3)当m的值变化时,动线段BC与线段OA的距离始终为1,线段BC的中点为G,
(3)当m的值变化时,动线段BC与线段OA的距离始终为1,线段BC的中点为G,
求点G随线段BC运动所走过的路径长是多少?


|
|
|
|
查看答案和解析>>
科目:初中数学 来源: 题型:
若一列不全为零的数除了第一个数和最后一个数外,每个数都等于前后与它相邻的两数之和,则称这列数具有“波动性质”.已知一列数共有18个,且具有“波动性质”,则这18个数的和为
A.-64 B.0 C.18 D.64
查看答案和解析>>
科目:初中数学 来源: 题型:
如果三角形有一边上的中线恰好等于这边的长,那么称这个三角形为“匀称三角形”
(1)已知:如图1,在△ABC中,∠C=90°,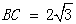 ,
,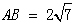 .
.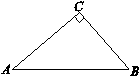
求证:△ABC是“匀称三角形”;
图1
(2)在平面直角坐标系xoy中,如果三角形的一边在x轴上,且这边的中线恰好等于这边的长,我们又称这个三角形为“水平匀称三角形”.如图2,现有10个边长是1的小正方形组成的长方形区域记为G, 每个小正方形的顶点称为格点,A(3,0),B(4,0),若C、D(C、D两点与O不重合)是x轴上的格点,且点C在点A的左侧. 在G内使△PAC与△PBD都是“水平匀称三角形”的点P共有几个?其中是否存在横坐标为整数的点P,如果存在请求出这个点P的坐标,如果不存在请说明理由.
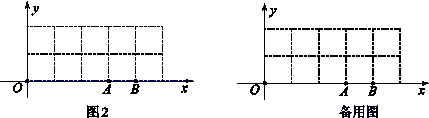
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com