
已知:如图(a),四边形ABCD是⊙O的内接四边形,A是![]() 的中点,过A点的切线与CB的延长线交于点E.
的中点,过A点的切线与CB的延长线交于点E.
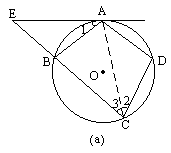
(1)求证:AB·DA=CD·BE;
(2)若点E在CB延长线上运动,点A在![]() 上运动,使切线EA变为割线EFA,其它条件不变,问具备什么条件可以使原结论成立?(要求画出示意图并注明条件,不要求证明.)
上运动,使切线EA变为割线EFA,其它条件不变,问具备什么条件可以使原结论成立?(要求画出示意图并注明条件,不要求证明.)
|
(1)证明:见图(a),连结AC. ∵A是 ∴ ∵EA切⊙O于点A,点C在⊙O上, ∴∠1=∠3=∠2. ∵四边形ABCD是⊙O的内接四边形, ∴∠ABE=∠D. ∴△ABE∽△CDA. ∴ ∴AB·DA=CD·BE. (2)解:如图(b),具备条件
|
|
要证明AB·DA=CD·BE,只要连结AC,证明这四条线段所在的两个三角形相似即可. 本题中第(2)小问是条件开放性试题,是在图形变化和运动中让考生探求所需的条件,既有新意,又加大了考查力度. |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).查看答案和解析>>
科目:初中数学 来源:2011-2012学年上海松江初一上学期12月月考数学试卷(带解析) 题型:解答题
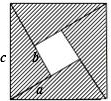
已知(如图):用四块底为b、高为a、斜边为c的直角三角形拼成一个正方形,求图形中央的小正方
形的面积,你不难找到
解法(1)小正方形的面积=
解法(2)小正方形的面积=
由解法(1)、(2),可以得到a、b、c的关系为: 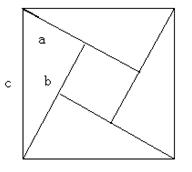
查看答案和解析>>
科目:初中数学 来源:2011-2012学年上海松江初一上学期12月月考数学试卷(解析版) 题型:解答题
已知(如图):用四块底为b、高为a、斜边为c的直角三角形拼成一个正方形,求图形中央的小正方
形的面积,你不难找到
解法(1)小正方形的面积=
解法(2)小正方形的面积=
由解法(1)、(2),可以得到a、b、c的关系为:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com