
| A. | 9 | B. | 5 | C. | 4 | D. | 4或14 |
分析 分两种情况讨论:锐角三角形和钝角三角形,根据勾股定理求得BD,CD,再由图形求出BC,在锐角三角形中,BC=BD+CD,在钝角三角形中,BC=CD-BD.
解答 解:(1)如图,锐角△ABC中,AB=15,AC=13,BC边上高AD=12,
在Rt△ABD中AB=15,AD=12,由勾股定理得:
BD2=AB2-AD2=152-122=81,
∴BD=9,
在Rt△ACD中AC=13,AD=12,由勾股定理得
CD2=AC2-AD2=132-122=25,
∴CD=5,
∴BC的长为BD+DC=9+5=14;
(2)钝角△ABC中,AB=15,AC=13,BC边上高AD=12,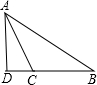
在Rt△ABD中AB=15,AD=12,由勾股定理得:
BD2=AB2-AD2=152-122=81,
∴BD=9,
在Rt△ACD中AC=13,AD=12,由勾股定理得:
CD2=AC2-AD2=132-122=25,
∴CD=5,
∴BC的长为DC-BD=9-5=4.
故BC长为14或4.
故选:D.
点评 本题考查了勾股定理,把三角形斜边转化到直角三角形中用勾股定理解答.掌握在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:选择题
| 第一列 | 第二列 | 第三列 | 第四列 | 第五列 | |
| 第1行 | 1 | 3 | 5 | 7 | |
| 第2行 | 15 | 13 | 11 | 9 | |
| 第3行 | 17 | 19 | 21 | 23 | |
| 第4行 | 29 | 27 | 25 | ||
| … |
| A. | 第252行第1列 | B. | 第252行第2列 | C. | 第253行第1列 | D. | 第253行第2列 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,某人到岛上去探宝,从A处登陆后先往北走9km,又往东走6km,再折回向北走3km,往西一拐,仅走1km就找到宝藏.问登陆点A与宝藏埋藏点B之间的距离是( )km.
如图所示,某人到岛上去探宝,从A处登陆后先往北走9km,又往东走6km,再折回向北走3km,往西一拐,仅走1km就找到宝藏.问登陆点A与宝藏埋藏点B之间的距离是( )km.| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | $2\sqrt{3}$ | C. | $2\sqrt{5}$ | D. | 以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a(a+1) | B. | $\frac{a(a+1)}{2}$ | C. | a(a-1) | D. | $\frac{a(a-1)}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3元 | B. | 2元 | C. | 1.5元 | D. | 1元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com