
【题目】设二次函数y1=a(x﹣x1)(x﹣x2)(a≠0,x1≠x2)的图象与一次函数y2=dx+e(d≠0)的图象交于点(x1 , 0),若函数y=y1+y2的图象与x轴仅有一个交点,则( )
A.a(x1﹣x2)=d
B.a(x2﹣x1)=d
C.a(x1﹣x2)2=d
D.a(x1+x2)2=d
【答案】B
【解析】解:∵一次函数y2=dx+e(d≠0)的图象经过点(x1 , 0),
∴dx1+e=0,
∴y2=d(x﹣x1),
∴y=y1+y2=a(x﹣x1)(x﹣x2)+d(x﹣x1)
=ax2﹣axx2﹣ax1x+ax1x2+dx﹣dx1
=ax2+(d﹣ax2﹣ax1)x+ax1x2﹣dx1
∵当x=x1时,y1=0,y2=0,
∴当x=x1时,y=y1+y2=0,
∵y=ax2+(d﹣ax2﹣ax1)x+ax1x2﹣dx1与x轴仅有一个交点,
∴y=y1+y2的图象与x轴的交点为(x1 , 0)
∴ ![]() =x1 ,
=x1 ,
化简得:a(x2﹣x1)=d
故选:B.
【考点精析】利用抛物线与坐标轴的交点对题目进行判断即可得到答案,需要熟知一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.


科目:初中数学 来源: 题型:
【题目】如图,有两根直杆隔河相对,杆CD高30m,杆AB高20m,两杆相距50m.现两杆上各有一只鱼鹰,它们同时看到两杆之间的河面上E处浮起一条小鱼,于是以同样的速度同时飞下来夺鱼,结果两只鱼鹰同时到达,叼住小鱼.问两杆底部距鱼的距离各是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上点A、点B对应的数分别为![]() 、6.
、6.
![]() 、B两点的距离是______;
、B两点的距离是______;
![]() 当
当![]() 时,求出数轴上点C表示的有理数;
时,求出数轴上点C表示的有理数;
![]() 一元一次方解应用题:点D以每秒4个单位长度的速度从点B出发沿数轴向左运动,点E以每秒3个单位长度的速度从点A出发沿数轴向右运动,点F从原点出发沿数轴运动,点D、点E、点F同时出发,t秒后点D、点E相距1个单位长度,此时点D、点F重合,求出点F的速度及方向.
一元一次方解应用题:点D以每秒4个单位长度的速度从点B出发沿数轴向左运动,点E以每秒3个单位长度的速度从点A出发沿数轴向右运动,点F从原点出发沿数轴运动,点D、点E、点F同时出发,t秒后点D、点E相距1个单位长度,此时点D、点F重合,求出点F的速度及方向.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(4,0),B(0,4 ![]() ),把一个直角三角尺DEF放在△OAB内,使其斜边FD在线段AB上,三角尺可沿着线段AB上下滑动.其中∠EFD=30°,ED=2,点G为边FD的中点.
),把一个直角三角尺DEF放在△OAB内,使其斜边FD在线段AB上,三角尺可沿着线段AB上下滑动.其中∠EFD=30°,ED=2,点G为边FD的中点.
(1)求直线AB的解析式;
(2)如图1,当点D与点A重合时,求经过点G的反比例函数y= ![]() (k≠0)的解析式;
(k≠0)的解析式;
(3)在三角尺滑动的过程中,经过点G的反比例函数的图象能否同时经过点F?如果能,求出此时反比例函数的解析式;如果不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆O在直径,AD,BC分别切⊙O于A,B两点,CD切⊙O于点E,连接OD,OC,下列结论:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2 , ④OD:OC=DE:EC,⑤OD2=DECD,正确的有( ) 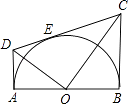
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
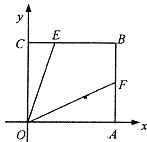
【题目】如图,在正方形OABC中,点B的坐标是(3,3),点E、F分别在边BC、BA上,CE=1,若∠EOF=45°,则F点的纵坐标是( )
A. 1 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A在函数 ![]() 的图象上,AB⊥
的图象上,AB⊥ ![]() 轴于点B,AB的垂直平分线与
轴于点B,AB的垂直平分线与 ![]() 轴交于点C,与函数
轴交于点C,与函数 ![]() 的图象交于点D。连结AC,CB,BD,DA,则四边形ACBD的面积等于( )
的图象交于点D。连结AC,CB,BD,DA,则四边形ACBD的面积等于( )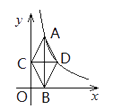
A. 2
B.![]()
C.4
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在全体丽水人民的努力下,我市剿灭劣V类水“河道清淤”工程取得了阶段性成果,下面的右表是全市十个县(市、区)指标任务数的统计表;左图是截止2017年3月31日和截止5月4日,全市十个县(市、区)指标任务累计完成数的统计图.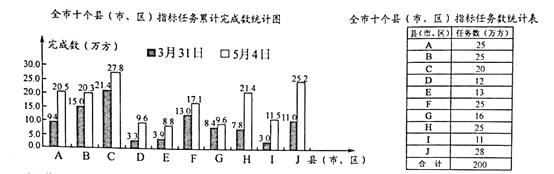
(1)截止3月31日,完成进度(完成进度=累计完成数÷任务数×100%)最快、电慢的县(市、区)分别是哪一个?
(2)求截止5月4日全市的完成进度;
(3)请结合图形信息和数据分析,对I且完成指标任务的行动过程和成果进行评价.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com