(1)已知x-y=2+a,y-z=2-a,且a2=7,试求x2+y2+z2-xy-yz-zx的值.
(2)已知对多项式2x3-x2-13x+k进行因式分解时有一个因式是2x+3,试求4k2+4k+1的值.
解:(1)∵x-y=2+a,y-z=2-a,
∴x-z=4,
∴(x-y)
2+(y-z)
2+(x-z)
2=(2+a)
2+(2-a)
2+4
2,
即x
2-2xy+y
2+y
2-2yz+z
2+x
2-2xz+z
2=4+4a+a
2+4-4a+a
2+16,
整理得,2(x
2+y
2+z
2-xy-yz-zx)=2(a
2+12),
∵a
2=7,
∴x
2+y
2+z
2-xy-yz-zx=7+12=19;
(2)设因式分解的另一个因式为x
2+ax+b,
则(2x+3)(x
2+ax+b)=2x
3+2ax
2+2bx+3x
2+3ax+3b=2x
3+(2a+3)x
2+(2b+3a)x+3b=2x
3-x
2-13x+k,
所以
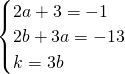
,
解得
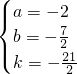
,
所以,4k
2+4k+1=(2k+1)
2=[2×(-

)+1]
2=(-20)
2=400.
分析:(1)把已知条件相加求出x-z=4,然后求出三个等式的平方和,再代入数据整理即可得解;
(2)设因式分解的另一个因式为x
2+ax+b,然后利用多项式的乘法运算法则展开,然后根据对应项系数相等列出方程组求出a、b、k的值,把多项式4k
2+4k+1利用完全平方公式进行因式分解,代入k的值进行计算即可得解.
点评:本题考查了完全平方公式以及因式分解的意义,(1)中观察出所求代数式是x、y、z三数的差的平方和是解题的关键,(2)中根据因式分解与多项式的乘法是互逆运算求出k的值是解题的关键.

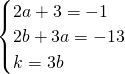 ,
,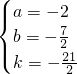 ,
, )+1]2=(-20)2=400.
)+1]2=(-20)2=400.

 4、如图为某班35名学生在某次社会实践活动中拣废弃的矿泉水瓶情况条形统计图,图中上面部分数据破损导致数据不完全.已知此次活动中学生拣到矿泉水瓶个数中位数是5个,则根据统计图,下列选项中的( )数值无法确定.
4、如图为某班35名学生在某次社会实践活动中拣废弃的矿泉水瓶情况条形统计图,图中上面部分数据破损导致数据不完全.已知此次活动中学生拣到矿泉水瓶个数中位数是5个,则根据统计图,下列选项中的( )数值无法确定.