
【题目】已知点![]() 为二次函数
为二次函数![]() 的图象的顶点.
的图象的顶点.
(1)过点![]() 作
作![]() 轴的垂线,垂足为点
轴的垂线,垂足为点![]() ,求线段
,求线段![]() 的最小值;
的最小值;
(2)设正比例函数![]() 与上述二次函数的图象相交于点
与上述二次函数的图象相交于点![]() ,
,![]() ,当
,当![]() 时,求
时,求![]() ,
,![]() 的值.
的值.
【答案】(1)PQ最小值为4;(2)k=2时m=-4;k=-2时,m=4.
【解析】
(1)将二次函救的解析式由一般式化为顶点式,用含![]() 的式子表示出顶点坐标,进而表示出线段
的式子表示出顶点坐标,进而表示出线段![]() 的长,并结合二次函数的性质求线段的最值;
的长,并结合二次函数的性质求线段的最值;
(2)易知点![]() ,
,![]() 关于原点对称,用含
关于原点对称,用含![]() 的式子表示出顶点
的式子表示出顶点![]() 的坐标后,根据对称性表示出点
的坐标后,根据对称性表示出点![]() 的坐标,将点
的坐标,将点![]() 的坐标代入二次函数的解析式求解即可得到
的坐标代入二次函数的解析式求解即可得到![]() 的值,进而得到点
的值,进而得到点![]() 的坐标,将点
的坐标,将点![]() 的坐标代入正比例函数的解析式即可得到
的坐标代入正比例函数的解析式即可得到![]() 的值.
的值.
(1)![]() ,
,![]() ,
,
![]() .
.
易得当![]() 时,
时,![]() 取得最小值,最小值为4.
取得最小值,最小值为4.
(2)![]() 是正比例函数,
是正比例函数,![]() ,
,
∴点![]() ,
,![]() 关于原点
关于原点![]() 对称,则
对称,则![]() .
.
将![]() 代入
代入![]() ,
,
得![]() ,解得
,解得![]() .
.
当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() .
.
∵点![]() 在正比例函数
在正比例函数![]() 的图象上,
的图象上,
![]()
当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() .
.
∵点![]() 在正比例函数
在正比例函数![]() 的图象上,
的图象上,
![]() .
.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
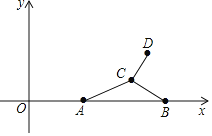
【题目】如图,在平面直角坐标系中,点A的坐标为(4,0),点B的坐标为(10,0),点C为平面上一动点,连接CA,CB,将线段CB绕点C逆时针旋转90°得到线段CD,当AC=4,线段AD的长取最大值时,点D的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年3月2日,500架无人飞机在西安创业咖啡街区的夜空绽放,西安高新区用“硬科技”打造了最具独特的风景线,2018“西安年,最中国”以一场华丽的视觉盛宴完美收官,当晚,某兴趣爱好者想用手中的无人机测量大雁塔的高度,如图是从大雁塔正南面看到的正视图,兴趣爱好者将无人机上升至离地面185米高大雁塔正东面的F点,此时,他测得F点都塔顶A点的俯视角为30°,同时也测得F点到塔底C点的俯视角为45°,已知塔底边心距OC=23米,请你帮助该无人机爱好者计算出大雁塔的大体高度(结果精确到0.1米)?(![]() ≈1.73,
≈1.73,![]() ≈1.41).
≈1.41).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋中装有相同的三个小球,其上面分别标注数字1、2、3、,现从中任意摸出一个小球,将其上面的数字作为点M的横坐标;将球放回袋中搅匀,再从中任意摸出一个小球,将其上面的数字作为点M的纵坐标.
(1)求点M在直线y=x上的概率;
(2)求点M的横坐标与纵坐标之和是偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市A,B两个蔬菜基地得知四川C,D两个灾民安置点分别急需蔬菜240t和260t的消息后,决定调运蔬菜支援灾区,已知A蔬菜基地有蔬菜200t,B蔬菜基地有蔬菜300t,现将这些蔬菜全部调运C,D两个灾区安置点.从A地运往C,D两处的费用分别为每吨20元和25元,从B地运往C,D两处的费用分别为每吨15元和18元.设从B地运往C处的蔬菜为x吨.
(1)请填写下表,并求两个蔬菜基地调运蔬菜的运费相等时x的值;
C | D | 总计/t | |
A | 200 | ||
B | x | 300 | |
总计/t | 240 | 260 | 500 |
(2)设A,B两个蔬菜基地的总运费为w元,求出w与x之间的函数关系式,并求
总运费最小的调运方案;
(3)经过抢修,从B地到C处的路况得到进一步改善,缩短了运输时间,运费每吨减少m元(m>0),其余线路的运费不变,试讨论总运费最小的调动方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
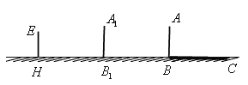
【题目】学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为![]() 的小明
的小明![]() 的影子
的影子![]() 长是
长是![]() ,而小颖
,而小颖![]() 刚好在路灯灯泡的正下方
刚好在路灯灯泡的正下方![]() 点,并测得
点,并测得![]() .
.
(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置![]() ;
;
(2)求路灯灯泡的垂直高度![]() ;
;
(3)如果小明沿线段BH向小颖(点H)走去,当小明走到BH中点B1处时,请在图中画出此时小明的影长B1C1,并求B1C1的长;
查看答案和解析>>
科目:初中数学 来源: 题型:
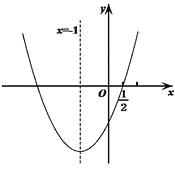
【题目】如图,二次函数![]() 的图象经过点
的图象经过点![]() ,对称轴为直线
,对称轴为直线![]() ,下列5个结论:①
,下列5个结论:①![]() ; ②
; ②![]() ; ③
; ③![]() ;④
;④![]() ; ⑤
; ⑤![]() ,其中正确的结论为________________.(注:只填写正确结论的序号)
,其中正确的结论为________________.(注:只填写正确结论的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com