
【题目】如图,已知在△ABC中,AB=AC,D是△ABC外接圆劣弧AC上的点(不与A,C重合),延长BD至E.
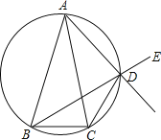
(1)求证:AD的延长线平分∠CDE;
(2)若∠BAC=30°,且△ABC底边BC边上高为1,求△ABC外接圆的周长.
【答案】(1)证明见解析;(2)4(2-![]() )π.
)π.
【解析】
(1)要证明AD的延长线平分∠CDE,即证明∠EDF=∠CDF,转化为证明∠ADB=∠CDF,再根据A,B,C,D四点共圆的性质,和等腰三角形角之间的关系即可得到.
(2)求△ABC外接圆的面积,只需解出圆半径,故作等腰三角形底边上的垂直平分线即过圆心,再连接OC,根据角之间的关系在三角形内即可求得圆半径,可得到外接圆面积.
(1)证明:如图,设F为AD延长线上一点,
∵A,B,C,D四点共圆,
∴∠CDF=∠ABC,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠ADB=∠ACB,
∴∠ADB=∠CDF,
∵∠ADB=∠EDF(对顶角相等),
∴∠EDF=∠CDF,
即AD的延长线平分∠CDE.
(2)设O为外接圆圆心,连接AO比延长交BC于H,连接OC,
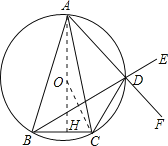
∵AB=AC,
∴![]() ,
,
∴AH⊥BC,
∴∠OAC=∠OAB=![]() ∠BAC=
∠BAC=![]() ×30°=15°,
×30°=15°,
∴∠COH=2∠OAC=30°,
设圆半径为r,
则OH=OCcos30°=![]() r,
r,
∵△ABC中BC边上的高为1,
∴AH=OA+OH=r+![]() r=1,
r=1,
解得:r=2(2-![]() ),
),
∴△ABC的外接圆的周长为:4(2-![]() )π.
)π.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
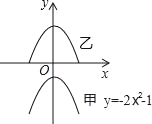
【题目】已知抛物线甲:y=﹣2x2﹣1和抛物线乙的形状相同,且两条抛物线的对称轴均为y轴,两点距离5个单位长度,它们的图象如图所示,则抛物线乙的解析式为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.

(1)求证:△CAE∽△CBF
(2)若BE=1,AE=2,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD∥BC,∠A=90°,AD=1cm,AB=3cm,BC=5cm,动点P从点B出发以1cm/s的速度沿BC的方向运动,动点Q从点C出发以2cm/s的速度沿CD方向运动,P、Q两点同时出发,当Q到达点D时停止运动,点P也随之停止,设运动的时间为ts(t>0)
(1)求线段CD的长;
(2)t为何值时,线段PQ将四边形ABCD的面积分为1:2两部分?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点A(﹣1,0),顶点坐标(1,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①abc>0;②3a+b<0;③﹣
与x轴交于点A(﹣1,0),顶点坐标(1,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①abc>0;②3a+b<0;③﹣![]() ≤a≤﹣1;④a+b≥am2+bm(m为任意实数);⑤一元二次方程
≤a≤﹣1;④a+b≥am2+bm(m为任意实数);⑤一元二次方程![]() 有两个不相等的实数根,其中正确的有( )
有两个不相等的实数根,其中正确的有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=BC,以BC为直径的⊙O与AC相交于点D,过点D作DE⊥AB交CB延长线于点E,垂足为点F.
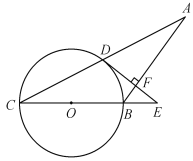
(1)判断DE与⊙O的位置关系,并说明理由;
(2)若⊙O的半径R=5,且tanC =![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△CDE均为等腰直角三角形,点B,C,D在一条直线上,点M是AE的中点,下列结论:①tan∠AEC=![]() ;②S△ABC+S△CDE≧S△ACE;③BM⊥DM;④BM=DM,正确结论的个数是( )
;②S△ABC+S△CDE≧S△ACE;③BM⊥DM;④BM=DM,正确结论的个数是( )
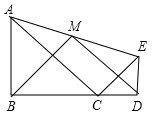
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:
①∠EBG=45°; ②△DEF∽△ABG;
③S△ABG=S△FGH; ④AG+DF=FG.
其中正确的是_____.(填写正确结论的序号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com