
����Ŀ����ͼ��ʾ���ı���ABCD�������Σ�M��AB�ӳ�����һ�㣮ֱ�����dzߵ�һ��ֱ�DZ߾�����D����ֱ�Ƕ���E��AB���ϻ�������E�����A��B�غϣ�����һֱ�DZ�����CBM��ƽ����BF�ཻ�ڵ�F��

��1����ͼ1������E��AB�ߵ��е�λ��ʱ��
��ͨ������DE��EF�ij��ȣ�����DE��EF�����������ϵ�� ��
�����ӵ�E��AD�ߵ��е�N������NE��BF�����������ϵ�� ����֤����IJ��룮
��2����ͼ2������E��AB���ϵ�����λ��ʱ�������ʱDE��EF��������������ϵ����֤����IJ��룮
���𰸡���1����DE=EF����NE=BF�����ɼ���������2��DE=EF�����ɼ�����.
�������������������1�����������ε����ʼ�N��E�ֱ�ΪAD��AB���е�ɵ�DN=EB���ٸ��ݽ�ƽ���ߵ����ʼ�AN=AE�ɵá�DNE=��EBF=135�㣬�Ӷ���֤�á�DNE�ա�EBF���̶�֤�ý��ۣ�
��2����DA���Ͻ�ȡDN=EB������NE����N��ʹ��NE=BF��������DN=EB�ɵ�AN=AE�����ݽ�ƽ���ߵ����ʿɵá�DNE=��EBF=90��+45��=135�㣬ͨ��֤��DNE�ա�EBF���Ӷ��ý���.
��1����DE=EF����NE=BF���������£�
���ı���ABCDΪ�����Σ���AD=AB����DAB=��ABC=90�㣬��N��E�ֱ�ΪAD��AB�е㣬
��AN=DN=![]() AD��AE=EB=
AD��AE=EB=![]() AB����DN=BE��AN=AE���ߡ�DEF=90�㣬���AED+��FEB=90�㣬
AB����DN=BE��AN=AE���ߡ�DEF=90�㣬���AED+��FEB=90�㣬
�֡ߡ�ADE+��AED=90�㣬���FEB=��ADE���֡�AN=AE�����ANE=��AEN���֡ߡ�A=90�����ANE=45�㣬���DNE=180�㩁��ANE=135�㣬�֡ߡ�CBM=90�㣬BFƽ�֡�CBM��
���CBF=45�㣬��EBF=135�㣬�ڡ�DNE�͡�EBF��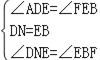 �� ���DNE�ա�EBF��ASA������DE=EF��NE=BF��
�� ���DNE�ա�EBF��ASA������DE=EF��NE=BF��
��2��DE=EF���������£�
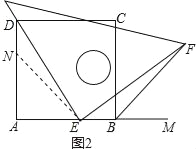
��DA���Ͻ�ȡDN=EB������NE�����ı���ABCD�������Σ�DN=EB����AN=AE�����AENΪ����ֱ�������Σ����ANE=45�㣬���DNE=180�㩁45��=135�㣬��BFƽ�֡�CBM��AN=AE�����EBF=90��+45��=135�㣬���DNE=��EBF�� �ߡ�NDE+��DEA=90�㣬��BEF+��DEA=90�㣬���NDE=��BEF���ڡ�DNE�͡�EBF��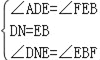 �����DNE�ա�EBF��ASA���� ��DE=EF��
�����DNE�ա�EBF��ASA���� ��DE=EF��


 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
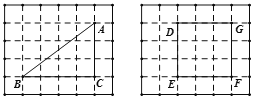
����Ŀ���ڱ߳�Ϊ1��С��������ɵķ���ֽ�У�������ε�ÿ�����㶼�ڷ���ֽ�ĸ�㣨���������ߵĽ����㣩�ϣ������Ķ���γ�Ϊ�������.�Ǹ�������ڵĸ����Ϊ![]() ���߽��ϵĸ����Ϊ
���߽��ϵĸ����Ϊ![]() ���������ε�����ɱ�ʾΪ
���������ε�����ɱ�ʾΪ![]() ������
������![]() ��
�� ![]() ����.
����.
��1������������ŷ���ֽ�и���һ��������Σ�����Ϊ![]() ��������
��������![]() .������һ����
.������һ���� ![]() �ڵĸ������_______��������
�ڵĸ������_______��������![]() �߽��ϵĸ������_______;
�߽��ϵĸ������_______;
��2�����ã�1���е������������ȷ��![]() ��
�� ![]() ��ֵ;
��ֵ;
��3������һ�ŷ���ֽ����110����㣬����һ��������Σ��������![]() �����ø��������ĸ����Ϊ
�����ø��������ĸ����Ϊ![]() .
.
����գ���![]() ����
����![]() ��������������
��������������
����![]() ����
����![]() ��ֵ��(д��������)
��ֵ��(д��������)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
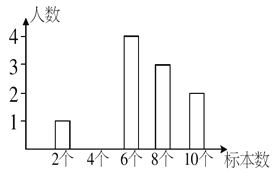
����Ŀ��ij�������С���ͬѧ����ֲ��걾�������������ͳ��������

���ݱ����ṩ����Ϣ���ش�����������
��1�����鹲��ѧ�������ˣ�
��2��ÿ�������걾����6�������ϵ�������ȫ����������ռ������
��3��ƽ��ÿ���������ٸ��걾��
��4����ȫ��ͼ������ͳ��ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ABCD�У�AB=4���Խ��߽��ڵ�O��F��BO���е㣬����AF����AF�ij��ȣ� 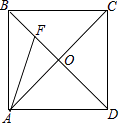
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�O���ڽ��ı���ACDB�У�ABΪֱ����AC��BC��1��2����DΪ![]() ���е㣬BE��CD����ΪE��
���е㣬BE��CD����ΪE��

(1)����BCE�Ķ�����
(2)��֤��DΪCE���е㣻
(3)����OE��BC�ڵ�F����AB��![]() ����OE�ij��ȣ�
����OE�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������A��B��C�����ʾ�����ֱ�Ϊ![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��
��
![]()
(1)��![]() = ��
= �� ![]() = ��
= ��
(2)����P��A���������ÿ��10����λ���ٶ������������˶�������B��ͣ��Ƭ�̺�������ÿ��6����λ���ٶ������᷵�ص�A�㣬������6�룻���д�C��B������ʱ��B��C(������B��ͣ����ʱ��)������2����
����C���ʾ����![]() ��
��
�����˶�ʱ��Ϊ![]() �룬��
�룬��![]() Ϊ��ֵʱ����P��A��B��C����ľ���֮��Ϊ23����λ��
Ϊ��ֵʱ����P��A��B��C����ľ���֮��Ϊ23����λ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2014��5�£��ж�����ǩ���˹���������ͬ����2018���𣬶���˹��ʼ���ҹ����������մﵽÿ��380�������ף�380����������ÿ�ѧ��������ʾΪ�� ��
A.3.8��109
B.3.8��1010
C.3.8��1011
D.3.8��1012
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У���E��BC���е㣬����ABE��AE�۵���õ���AFE����F��������ABCD���ڲ����ӳ�AF��CD�ڵ�G��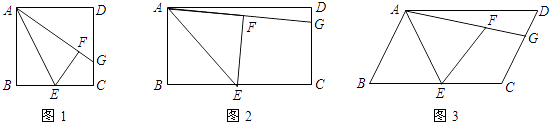
��1�����벢֤���߶�GF��GC��������ϵ��
��2������ͼ1�е������θijɾ��Σ������������䣬��ͼ2����ô�߶�GF��GC֮���������ϵ�Ƿ�ı䣿��֤����Ľ��ۣ�
��3������ͼ1�е������θij�ƽ���ı��Σ������������䣬��ͼ3����ô�߶�GF��GC֮���������ϵ�Ƿ��ı䣿��֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com