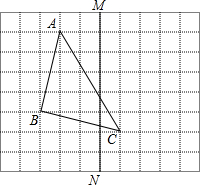练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．如图，在正方形网格上有一个△ABC．
    （1）画出△ABC关于直线MN的对称图形（不写画法）；
    （2）若网格上的每个小正方形的边长为1，则△ABC的面积为$\frac{17}{2}$．

    分析 （1）先利用网格确定△ABC关于直线MN对称的点，再顺次连接各点即可得到△ABC关于直线MN的对称图形；
    （2）根据△ABC是等腰直角三角形，由勾股定理可知腰长为$\sqrt{17}$，即可得到△ABC的面积．

    解答 解：（1）如图所示，△DEF即为所求；

    （2）△ABC的面积=$\frac{1}{2}$×$\sqrt{17}$×$\sqrt{17}$=$\frac{17}{2}$．
    故答案为：$\frac{17}{2}$．

    点评 本题主要考查了利用轴对称变换进行作图，画一个图形的轴对称图形时，是先从确定一些特殊的对称点开始的．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    20．（1）如图1，已知△ABC中，以B、C为圆心，以大于$\frac{1}{2}$BC长为半径画弧相交于M、N两点，连接MN交BC于点D，则线段BD与CD的数量关系为BD=CD．
    （2）在（1）的基础上，取AB的中点E，连接DE并延长到F，使EF=DE，连接AF、BF、AD，得到图2．
    ①求证：四边形AFDC是平行四边形．
    ②当∠BAC=90°时，求证：AF=AD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

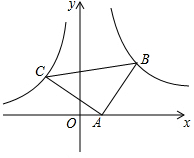    1．如图，点B（3，3）在双曲线y=$\frac{k}{x}$（x＞0）上，点C在双曲线y=-$\frac{4}{x}$（x＜0）上，点A在x轴的正半轴上，且△ABC是以BC为斜边的等腰直角三角形．
    （1）填空：k=9；
    （2）求点A的坐标；
    （3）若点D是x轴上一点，且以点D、O、C为顶点的三角形是等腰三角形，请直接写出点D的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

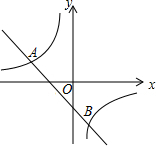    18．如图，在平面直角坐标系xOy中，直线y=kx+b（k≠0）与反比例函数y=$\frac{m}{x}$（m≠0）交于点A（-4，n）和点B（2，-4）．
    （1）求反比例函数的表达式及n的值；
    （2）根据图象写出不等式kx+b-$\frac{m}{x}$＜0的解集．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

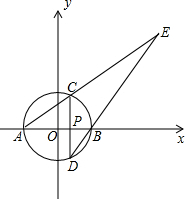    5．如图，以原点O为圆心，3为半径的圆与x轴分别交于A，B两点（点B在点A的右边），P是半径OB上一点，过P且垂直于AB的直线与⊙O分别交于C，D两点（点C在点D的上方），直线AC，DB交于点E．若AC：CE=1：2．
    （1）求点P的坐标；
    （2）求过点A和点E，且顶点在直线CD上的抛物线的函数表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

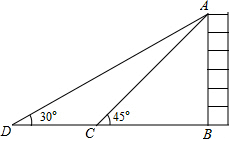    15．如图所示，为了测量出一垂直水平地面的某高大建筑物AB的高度，一测量人员在该建筑物附近C处，测得建筑物顶端A处的仰角大小为45°，随后沿直线BC向前走了100米后到达D处，在D处测得A处的仰角大小为30°，则建筑物AB的高度约为137米．
    （注：不计测量人员的身高，结果按四舍五入保留整数，参考数据：$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．若y=$\sqrt{x-\frac{1}{2}}$+$\sqrt{\frac{1}{2}-x}$-6，则xy=-3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．正方形ABCD的边长为1，点O是BC边上的一个动点（与B，C不重合），以O为顶点在BC所在直线的上方作∠MON=90°．
    （1）当OM经过点A时，
    ①请直接填空：ON不可能（可能，不可能）过D点；（图1仅供分析）
    ②如图2，在ON上截取OE=OA，过E点作EF垂直于直线BC，垂足为点F，作EH⊥CD于H，求证：四边形EFCH为正方形．
    （2）当OM不过点A时，设OM交边AB于G，且OG=1．在ON上存在点P，过P点作PK垂直于直线BC，垂足为点K，使得S△PKO=4S△OBG，连接GP，求四边形PKBG的最大面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

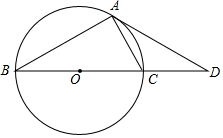    20．如图，已知BC是⊙O的直径，点D为BC延长线上的一点，点A为圆上一点，且AB=AD，AC=CD．
    （1）求证：△ACD∽△BAD；
    （2）求证：AD是⊙O的切线．

    查看答案和解析>>

    同步练习册答案