
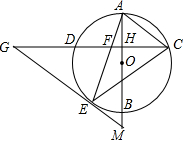
 如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过$\widehat{BD}$上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过$\widehat{BD}$上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.分析 (1)由AC∥EG,推出∠G=∠ACG,由AB⊥CD推出$\widehat{AD}$=$\widehat{AC}$,推出∠CEF=∠ACD,推出∠G=∠CEF,由此即可证明;
(2)欲证明EG是⊙O的切线只要证明EG⊥OE即可;
(3)连接OC.设⊙O的半径为r.在Rt△OCH中,利用勾股定理求出r,证明△AHC∽△MEO,可得$\frac{AH}{EM}$=$\frac{HC}{OE}$,由此即可解决问题;
解答 (1)证明:如图1中,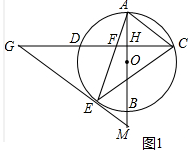
∵AC∥EG,
∴∠G=∠ACG,
∵AB⊥CD,
∴$\widehat{AD}$=$\widehat{AC}$,
∴∠CEF=∠ACD,
∴∠G=∠CEF,∵∠ECF=∠ECG,
∴△ECF∽△GCE.
(2)证明:如图2中,连接OE,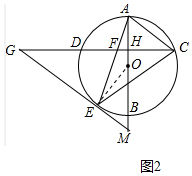
∵GF=GE,
∴∠GFE=∠GEF=∠AFH,
∵OA=OE,
∴∠OAE=∠OEA,
∵∠AFH+∠FAH=90°,
∴∠GEF+∠AEO=90°,
∴∠GEO=90°,
∴GE⊥OE,
∴EG是⊙O的切线.
(3)解:如图3中,连接OC.设⊙O的半径为r.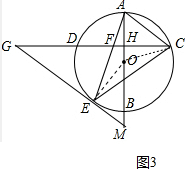
在Rt△AHC中,tan∠ACH=tan∠G=$\frac{AH}{HC}$=$\frac{3}{4}$,
∵AH=3$\sqrt{3}$,
∴HC=4$\sqrt{3}$,
在Rt△HOC中,∵OC=r,OH=r-3$\sqrt{3}$,HC=4$\sqrt{3}$,
∴(r-3$\sqrt{3}$)2+(4$\sqrt{3}$)2=r2,
∴r=$\frac{25\sqrt{3}}{6}$,
∵GM∥AC,
∴∠CAH=∠M,∵∠OEM=∠AHC,
∴△AHC∽△MEO,
∴$\frac{AH}{EM}$=$\frac{HC}{OE}$,
∴$\frac{3\sqrt{3}}{EM}$=$\frac{4\sqrt{3}}{\frac{25\sqrt{3}}{6}}$,
∴EM=$\frac{25\sqrt{3}}{8}$.
点评 本题考查圆综合题、垂径定理、相似三角形的判定和性质、锐角三角函数、勾股定理等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题,正确寻找相似三角形,构建方程解决问题吗,属于中考压轴题.


科目:初中数学 来源: 题型:填空题
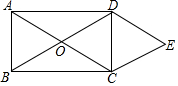 如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC,AD=2$\sqrt{3}$,DE=2,下列结论:①AB=2;②∠E=45°;③四边形OCED是菱形;④四边形OCED的面积为2$\sqrt{3}$,其中正确的是①③④(把所有正确结论的序号都填上).
如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC,AD=2$\sqrt{3}$,DE=2,下列结论:①AB=2;②∠E=45°;③四边形OCED是菱形;④四边形OCED的面积为2$\sqrt{3}$,其中正确的是①③④(把所有正确结论的序号都填上).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
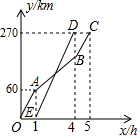 小明家和邻居李叔叔家计划分别驾车去离家270km处的某景点旅游,商量好早上7:00出发,李叔叔因家中有事,8:00才出发,于是小明家便减慢了速度,为了追上小明家,李叔叔加快了行驶速度,结果比小明家先到,小明家知道后便以最初的速度全力向景区驶去,己知他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示.
小明家和邻居李叔叔家计划分别驾车去离家270km处的某景点旅游,商量好早上7:00出发,李叔叔因家中有事,8:00才出发,于是小明家便减慢了速度,为了追上小明家,李叔叔加快了行驶速度,结果比小明家先到,小明家知道后便以最初的速度全力向景区驶去,己知他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
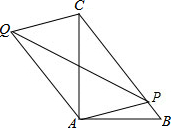 如图,Rt△ABC中,∠BAC=90°,AB=6,AC=8,点P为BC上任意一点,连接PA,以PA、PC为邻边作平行四边形PAQC,连接PQ,则PQ的最小值为$\frac{24}{5}$.
如图,Rt△ABC中,∠BAC=90°,AB=6,AC=8,点P为BC上任意一点,连接PA,以PA、PC为邻边作平行四边形PAQC,连接PQ,则PQ的最小值为$\frac{24}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
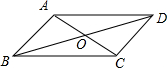 如图,平行四边形ABCD的对角线AC,BD交于点O,AC⊥AB,AB=2,且AC:BD=1:2,
如图,平行四边形ABCD的对角线AC,BD交于点O,AC⊥AB,AB=2,且AC:BD=1:2,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知BD是△ABC的角平分线,DE∥AB交BC于E,EF∥AC交AB于F.
如图,已知BD是△ABC的角平分线,DE∥AB交BC于E,EF∥AC交AB于F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
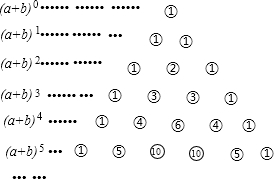
| A. | 2017 | B. | 2016 | C. | 191 | D. | 190 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
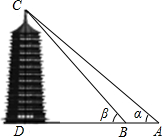 一数学兴趣小组来到某公园,准备测量一座塔的高度.如图,在A处测得塔顶的仰角为α,在B处测得塔顶的仰角为β,又测量出A、B两点的距离为s米,则塔高为$\frac{tanα•tanβ•s}{tanβ-tanα}$米.
一数学兴趣小组来到某公园,准备测量一座塔的高度.如图,在A处测得塔顶的仰角为α,在B处测得塔顶的仰角为β,又测量出A、B两点的距离为s米,则塔高为$\frac{tanα•tanβ•s}{tanβ-tanα}$米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
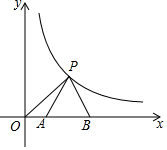 如图,P(m,m)是反比例函数y=$\frac{9}{x}$在第一象限内的图象上一点,以P为顶点作等边△PAB,使AB落在x轴上,则△POB的面积为( )
如图,P(m,m)是反比例函数y=$\frac{9}{x}$在第一象限内的图象上一点,以P为顶点作等边△PAB,使AB落在x轴上,则△POB的面积为( )| A. | $\frac{9}{2}$ | B. | 3$\sqrt{3}$ | C. | $\frac{9+12\sqrt{3}}{4}$ | D. | $\frac{9+3\sqrt{3}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com