【题目】已知一个不透明的袋子中装有7个只有颜色不同的球，其中2个白球，5个红球．
（1）求从袋中随机摸出一个球是红球的概率．
（2）从袋中随机摸出一个球，记录颜色后放回，摇匀，再随机摸出一个球，求两次摸出的球恰好颜色不同的概率．
（3）若从袋中取出若干个红球，换成相同数量的黄球．搅拌均匀后，使得随机从袋中摸出两个球，颜色是一白一黄的概率为
，求袋中有几个红球被换成了黄球．
【答案】（1）
；（2）
；（3）袋中有3个红球被换成了黄球．
【解析】
（1）直接利用概率公式计算可得；
（2）先列表得出所有等可能结果，再从中找到符合条件的结果数，继而利用概率公式求解可得；
（3）设有x个红球被换成了黄球，根据颜色是一白一黄的概率为
列出关于x的方程，解之可得．
（1）∵袋中共有7个小球，其中红球有5个，
∴从袋中随机摸出一个球是红球的概率为；
（2）列表如下：
白 | 白 | 红 | 红 | 红 | 红 | 红 | |
白 | （白，白） | （白，白） | （白，红） | （白，红） | （白，红） | （白，红） | （白，红） |
白 | （白，白） | （白，白） | （白，红） | （白，红） | （白，红） | （白，红） | （白，红） |
红 | （白，红） | （白，红） | （红，红） | （红，红） | （红，红） | （红，红） | （红，红）/span> |
红 | （白，红） | （白，红） | （红，红） | （红，红） | （红，红） | （红，红） | （红，红） |
红 | （白，红） | （白，红） | （红，红） | （红，红） | （红，红） | （红，红） | （红，红） |
红 | （白，红） | （白，红） | （红，红） | （红，红） | （红，红） | （红，红） | （红，红） |
红 | （白，红） | （白，红） | （红，红） | （红，红） | （红，红） | （红，红） | （红，红） |
由表知共有49种等可能结果，其中两次摸出的球恰好颜色不同的有20种结果，
∴两次摸出的球恰好颜色不同的概率为
（3）设有x个红球被换成了黄球．
根据题意，得：
，
解得：x＝3，
即袋中有3个红球被换成了黄球．
科目：初中数学 来源： 题型：
【题目】如图，矩形ABCD中，E是BC上一点，连接AE，将矩形沿AE翻折，使点B落在CD边F处，连接AF，在AF上取点O，以O为圆心，OF长为半径作⊙O与AD相切于点P．若AB＝6，BC＝3
，则下列结论：①F是CD的中点；②⊙O的半径是2；③AE＝
CE；④S阴影＝
．其中正确的个数为（ ）
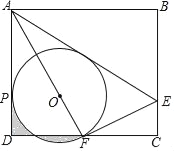
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下面是小东设计的“在三角形一边上求作一个点，使这点和三角形的两个顶点构成的三角形与原三角形相似”的尺规作图过程．
已知：△ABC．
求作：在BC边上求作一点P，使得△PAC∽△ABC．
作法：如图，
①作线段AC的垂直平分线GH；
②作线段AB的垂直平分线EF，交GH于点O；
③以点O为圆心，以OA为半径作圆；
④以点C为圆心，CA为半径画弧，交⊙O于点D（与点A不重合）；
⑤连接线段AD交BC于点P．
所以点P就是所求作的点．
根据小东设计的尺规作图过程，
（1）使用直尺和圆规，补全图形；（保留作图痕迹）
（2）完成下面的证明．
证明：∵CD＝AC，
∴
＝ ．
∴∠ ＝∠ ．
又∵∠ ＝∠ ，
∴△PAC∽△ABC（ ）（填推理的依据）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】潮州旅游文化节开幕前，某凤凰茶叶公司预测今年凤凰茶叶能够畅销，就用32000元购进了一批凤凰茶叶，上市后很快脱销，茶叶公司又用68000元购进第二批凤凰茶叶，所购数量是第一批购进数量的2倍，但每千克凤凰茶叶进价多了10元．
（1）该凤凰茶叶公司两次共购进这种凤凰茶叶多少千克？
（2）如果这两批茶叶每千克的售价相同，且全部售完后总利润率不低于20%，那么每千克售价至少是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形ABCD中，AB=6，BC=8，沿直线MN对折，使A、C重合，直线MN交AC于O．
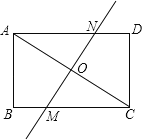
（1）求证：△COM∽△CBA；
（2）求线段OM的长度．
查看答案和解析>>
科目：初中数学 来源： 题型：
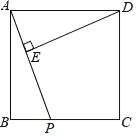
【题目】如图，在正方形ABCD中，AB＝4，P是BC边上一动点（不与B，C重合），DE⊥AP于E．
（1）试说明△ADE∽△PAB；
（2）若PA＝x，DE＝y，请写出y与x之间的函数关系式．
查看答案和解析>>
科目：初中数学 来源： 题型：
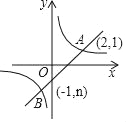
【题目】如图，一次函数y＝kx+b的图象与反比例函数y＝
的图象交于A、B两点．
（1）利用图中的条件，求反比例函数和一次函数的解析式．
（2）求△AOB的面积．
（3）根据图象直接写出使一次函数的值大于反比例函数的值的x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，点D、E分别在边AB、AC上，DE∥BC，∠ACD＝∠B，那么下列判断中，不正确的是（ ）
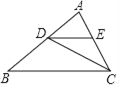
A. △ADE∽△ABC B. △CDE∽△BCD C. △ADE∽△ACD D. △ADE∽△DBC
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在四边形ABCD中，点E为AB边上的一点，点F为对角线BD上的一点，且EF⊥AB．若四边形ABCD为正方形．
①如图1，请直接写出AE与DF的数量关系 ；
②将△EBF绕点B逆时针旋转到图2所示的位置，连接AE，DF，猜想AE与DF的数量关系并说明理由．
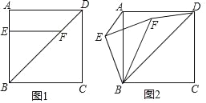
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com