
分析 根据数乘向量的几何意义,可得线段AB平行于线段CD,且AB长度是CD长度的$\frac{2}{3}$,得到四边形ABCD是梯形,又因为两腰|$\overrightarrow{AD}$|=|$\overrightarrow{BC}$|相等,可得四边形ABCD是等腰梯形.
解答 解:∵非零向量$\overrightarrow{AB}$=2$\overrightarrow{e}$,$\overrightarrow{DC}$=3$\overrightarrow{e}$(e≠0),
∴$\overrightarrow{AB}$∥$\overrightarrow{DC}$,且|$\overrightarrow{AB}$|=$\frac{2}{3}$|$\overrightarrow{DC}$|,
即线段AB平行于线段CD,且线段AB长度是线段CD长度的$\frac{2}{3}$,
∴四边形ABCD为以AB为上底、CD为下底的梯形,
又|$\overrightarrow{AD}$|=|$\overrightarrow{BC}$|,
∴梯形ABCD的两腰相等,
因此四边形ABCD是等腰梯形.
点评 本题考查了平面向量,此题给出四边形ABCD满足的向量等式,判断四边形ABCD的形状,着重考查了向量平行(共线)的条件与数学表达式、等腰梯形的定义等知识,属于基础题.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源: 题型:解答题
 如图,操场上有一根旗杆AH,为测量它的高度,在B和D处各立一根高1.5米的标杆BC、DE,两杆相距30米,测得视线AC与地面的交点为F,视线AE与地面的交点为G,并且H、B、F、D、G都在同一直线上,测得BF为3米,DG为5米,求旗杆AH的高度?
如图,操场上有一根旗杆AH,为测量它的高度,在B和D处各立一根高1.5米的标杆BC、DE,两杆相距30米,测得视线AC与地面的交点为F,视线AE与地面的交点为G,并且H、B、F、D、G都在同一直线上,测得BF为3米,DG为5米,求旗杆AH的高度?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
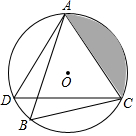 如图,在⊙O中,$\widehat{AD}$=$\widehat{AC}$,弦AB与弦AC相交于点A,弦CD与弦AB相交于点F,连接BC,其中CD=2$\sqrt{3}$cm,∠B=60°,求阴影部分的面积.
如图,在⊙O中,$\widehat{AD}$=$\widehat{AC}$,弦AB与弦AC相交于点A,弦CD与弦AB相交于点F,连接BC,其中CD=2$\sqrt{3}$cm,∠B=60°,求阴影部分的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
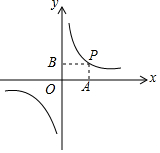 反比例函数y=$\frac{8}{x}$的图象如图所示,在第一象限的图象上任取一点P(x,y),作PA⊥x轴于点A,PB⊥y轴于点B.
反比例函数y=$\frac{8}{x}$的图象如图所示,在第一象限的图象上任取一点P(x,y),作PA⊥x轴于点A,PB⊥y轴于点B.| x | … | $\frac{1}{2}$ | 1 | 2 | 3 | 4 | 5 | … |
| y | … | … | ||||||
| S四边形OAPB | … | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com