

分析 (1)根据已知条件得到四边形ABCD是矩形,由矩形的性质得到∠A=∠FDC=90°,根据相似三角形的性质得到∠CFD=∠AED,根据余角的性质即可得到结论;
(2)根据已知条件得到△DFG∽△DEA,推出$\frac{DE}{AD}$=$\frac{DF}{DG}$,根据△CGD∽△CDF,得到$\frac{DF}{DG}$=$\frac{CF}{CD}$,等量代换即可得到结论;
(3)过C作CN⊥AD于N,CM⊥AB交AB延长线于M,连接BD,设CN=x,△BAD≌△BCD,推出∠BCD=∠A=90°,证△BCM∽△DCN,求出CM=$\frac{3}{4}$x,在Rt△CMB中,由勾股定理得出BM2+CM2=BC2,解方程得到CN,证出△AED∽△NFC,即可得出答案.
解答 (1)证明:∵AB∥CD,AB=CD,∠A=90°,
∴四边形ABCD是矩形,
∴∠A=∠FDC=90°,
∵AD•DF=AE•DC,
∴$\frac{AD}{AE}=\frac{CD}{DF}$,
∴△AED∽△DFC,
∴∠CFD=∠AED,
∵∠ADE+∠AED=90°,
∴∠ADE+∠CFD=90°,
∴∠DGF=90°,
∴DE⊥CF;
(2)证明:∵∠A=∠EGC,∠ADE=∠GDF,
∴△DFG∽△DEA,
∴$\frac{DE}{AD}$=$\frac{DF}{DG}$,
∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,∠AED=∠EDC,
∴∠B=∠ADC,
∵△DFG∽△DEA,
∴∠AED=∠DFG,
∴DFC=∠GDC,
∵∠DCG=∠FCD,
∴△CGD∽△CDF,
∴$\frac{DF}{DG}$=$\frac{CF}{CD}$,
∴$\frac{DE}{AD}$=$\frac{CF}{CD}$,
∴DE•CD=CF•DA;
(3)解:$\frac{DE}{CF}$为定值,
理由:过C作CN⊥AD于N,CM⊥AB交AB延长线于M,连接BD,设CN=x,
∵∠BAD=90°,即AB⊥AD,
∴∠A=∠M=∠CNA=90°,
∴四边形AMCN是矩形,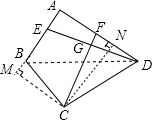
∴AM=CN,AN=CM,
∵在△BAD和△BCD中,$\left\{\begin{array}{l}{AD=CD}\\{AB=BC}\\{BD=BD}\end{array}\right.$,
∴△BAD≌△BCD(SSS),
∴∠BCD=∠A=90°,
∴∠ABC+∠ADC=180°,
∵∠ABC+∠CBM=180°,
∴∠MBC=∠ADC,
∵∠CND=∠M=90°,
∴△BCM∽△DCN,
∴$\frac{CM}{CN}$=$\frac{BC}{CD}$,
∴$\frac{CM}{x}=\frac{3}{4}$,
∴CM=$\frac{3}{4}$x,
在Rt△CMB中,CM=$\frac{3}{4}$x,BM=AM-AB=x-3,由勾股定理得:BM2+CM2=BC2,
∴(x-3)2+($\frac{3}{4}$x)2=32,
x=0(舍去),x=$\frac{96}{25}$,
∴CN=$\frac{96}{25}$,
∵∠A=∠FGD=90°,
∴∠AED+∠AFG=180°,
∵∠AFG+∠NFC=180°,
∴∠AED=∠CFN,
∵∠A=∠CNF=90°,
∴△AED∽△NFC,
∴$\frac{DE}{CF}$=$\frac{AD}{CN}$=$\frac{4}{\frac{96}{25}}$=$\frac{25}{24}$.
点评 本题考查了矩形性质和判定,勾股定理,平行四边形的性质和判定,全等三角形的性质和判定,相似三角形的性质和判定的应用,主要考查学生综合运用性质和定理进行推理的能力,题目比较好.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:解答题
 平行四边形ABCD在平面直角坐标系中的位置如图所示,已知AB=8,AD=6,∠BAD=60°,点A的坐标为(-2,0).求:
平行四边形ABCD在平面直角坐标系中的位置如图所示,已知AB=8,AD=6,∠BAD=60°,点A的坐标为(-2,0).求:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 时间(小时) | 5 | 6 | 7 | 8 | 9 |
| 人数 | 3 | 5 | 10 | 1 | 1 |
| A. | 6.6,10 | B. | 7,7 | C. | 6.6,7 | D. | 7,10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
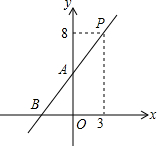 已知:如图,直线y=kx+4(k≠0)经过点A,B,P.
已知:如图,直线y=kx+4(k≠0)经过点A,B,P.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com